Def  x:A. B(x) == x:AB(x)

is mentioned by

Thm*  e:(BB).  Thm*  (b:B. e(b) = b) Thm*   Thm*  (A:Type, f:(AAB). (a:A. (Diag f wrt x. e(x)) = f(a)))	[diagonalization_wrt_eq]
Thm*  R:(BBProp), e:(BB). Thm*  (b:B. R(e(b),b)) Thm*   Thm*  (A:Type, f:(AAB). (a:A. R((Diag f wrt x. e(x))(a),f(a,a))))	[diagonalization]
Thm*  f:(AB). f  A{y:B| x:A. f(x) = y }	[range_restriction_indep]
Thm*  (x:A. !y:B. P(x,y))  (f:(AB). x:A. P(x,f(x)))	[indep_fun_description]
Thm*  (x:A. y:B. Q(x,y))  (f:(AB). x:A. Q(x,f(x)))	[ax_choice_version3]
Thm*  (x:A. y:B. Q(x,y))  (f:(AB). x:A. Q(x,f(x)))	[ax_choice_version2]
Thm*  (x:A. !y:B(x). P(x,y))  (f:(x:AB(x)). x:A. P(x,f(x)))	[fun_description]
Thm*  (x:A. y:B(x). Q(x,y))  (f:(x:AB(x)). x:A. Q(x,f(x)))	[dep_ax_choice_version2]
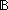Thm*  (x:T. Dec(E(x)))  (f:(T). x:T. f(x)  E(x))	[dec_pred_iff_some_boolfun]
Thm*  (Set:Type, :(SetSetProp). Thm*  (P:(SetProp). p:Set. x:Set. (x  p)  P(x))	[RussellsParadox_Frege2]
Thm*  (A:Type, Q:(AAProp). P:(AProp). p:A. x:A. Q(x,p)  P(x))	[RussellsParadox_Frege]
Thm*  (A Discrete)  (e:(AA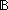). IsEqFun(A;e))	[discrete_vs_bool2]
Thm*  (A Discrete)  (e:(AA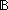). x,y:A. (x e y)  x = y)	[discrete_vs_bool]
Thm*  (!A)  (x:A. y:A. x = y)	[inhabited_uniquely_elim]
Thm*  (!A)  (x:A. y:A. x = y)	[inhabited_uniquely_vs_exists]
Thm*  (A)  (x:A. True)	[inhabited_vs_exists]
Thm*  A:Type. P = (A)  Prop	[inhab_rep_axiom]
Thm*  (x:T. Q(x))  (x:T. Q(x))	[not_over_exists_imp]
Thm*  Dec(P)  (b:. b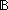  P)	[decbl_iff_some_bool]
Def  !x:A. P(x) == x:A. x is the x:A. P(x)	[exists_unique]

In prior sections: core quot 1

Try larger context: DiscrMathExt IF YOU CAN SEE THIS go to /sfa/Nuprl/Shared/Xindentation_hack_doc.html