Selected Objects
| THM | negnegelim_vs_bivalence
|
Double negation elimination is equivalent to bivalence.
( P:Prop. P:Prop.   P P   P) P)   ( ( P:Prop. P P:Prop. P 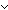  P) P) |
| THM | disjunct_elim
|
P 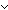 Q Q    P P   Q Q |
| THM | or_fused
|
Q 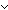 Q Q   Q Q |
| THM | guarded_prop_to_prop
|
The precise type of implication
 Q:Prop(given P). P Q:Prop(given P). P   Q Q  Prop Prop |
| THM | decidable__cand
|
 Q:Prop(given P). Dec(P) Q:Prop(given P). Dec(P)   (P (P   Dec(Q)) Dec(Q))   Dec(P & Q) Dec(P & Q) |
| THM | cand_is_prop
|
 B:Prop(given A). (A & B) B:Prop(given A). (A & B)  Prop Prop |
| def | equiv_rel_sep
|
EquivRel on A, R == EquivRel u,v:A. R(u,v) |
| def | allst
|
 x:A st P(x). Q(x) == x:A st P(x). Q(x) ==  x:A. P(x) x:A. P(x)   Q(x) Q(x) |
| def | allst_implicit
|
Q(x) ==  x:A st P(x). Q(x) x:A st P(x). Q(x) |
| def | product_conventional_notation
|
product_conventional_notation(A; x.B(x)) == x:A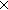 B(x) B(x) |
| def | quotient_sep
|
A/E == u,v:A//E(u,v) |
| THM | decbl_iff_some_bool
|
Dec(P)   ( ( b: b: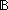 . b . b   P) P) |
| def | isect_two
|
Intersection of two types
A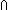 B == B == 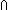 i: i: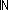 2. if i= 2. if i=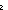 0 0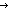 A else B fi A else B fi |
| THM | not_over_exists_imp
|
 ( ( x:T. Q(x)) x:T. Q(x))   ( ( x:T. x:T.  Q(x)) Q(x)) |
| def | exteq
|
Extensional equality between types
A =ext B == ( x:A. x x:A. x  B) & ( B) & ( x:B. x x:B. x  A) A) |
| THM | exteq_sigma_st_dom
|
 B:(A B:(A  Type), P:(A Type), P:(A  Prop). Prop).
(i:{i:A| P(i) }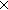 B(i)) =ext {v:(i:A B(i)) =ext {v:(i:A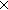 B(i))| P(v/x,y. x) } B(i))| P(v/x,y. x) } |
| THM | singleton_eq_in_self
|
 x:{a:A}. x = a x:{a:A}. x = a  {a:A} {a:A} |
| THM | singleton_singleton_self
|
{a:{a:A}} =ext {a:A} |
| def | fun_over_st
|
x:A st P(x)  B(x) == x:{x:A| P(x) } B(x) == x:{x:A| P(x) }  B(x) B(x) |
| def | inhabited
|
(type A has a member)
  A == A A == A |
| THM | inhab_choice
|
( x:A. x:A.   B(x)) B(x))   ( (  (x:A (x:A  B(x))) B(x))) |
| THM | inhab_rep_axiom
|
 A:Type{i}. P = ( A:Type{i}. P = (  A) A)  Prop Prop |
| THM | inhab_rep_eqv
|
 F:(Prop{i} F:(Prop{i}  Prop{j}). ( Prop{j}). ( P:Prop{i}. F(P)) P:Prop{i}. F(P))   ( ( A:Type{i}. F( A:Type{i}. F(  A)) A)) |
| THM | inhabited_vs_exists
|
(  A) A)   ( ( x:A. True) x:A. True) |
| def | inhabited_uniquely
|
(type A has exactly one member)
 ! ! A == A ==   {x:A| {x:A|  y:A. x = y } y:A. x = y } |
| THM | inhabited_uniquely_vs_exists
|
( ! ! A) A)   ( ( x:A. x:A.  y:A. x = y) y:A. x = y) |
| THM | inhabited_uniquely_elim
|
( ! ! A) A)   ( ( x:A. x:A.  y:A. x = y) y:A. x = y) |
| THM | unique_fn_over_empty
|
 ( (  A) A)   ( ( ! ! (A (A  B)) B)) |
| THM | not_sq_iff_sq
|
 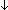 P P    P P |
| THM | sq_not_iff_sq
|
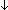 ( ( P) P)    P P |
| THM | dec_imp_dec_sq
|
Dec(P)   Dec( Dec(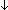 P) P) |
| THM | sq_sq_iff_sq
|
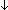 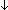 P P   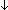 P P |
| THM | set_inc_wrt_imp
|
( x:A. B(x) x:A. B(x)   B'(x)) B'(x))   {x:A| B(x) } {x:A| B(x) } 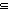 {x:A| B'(x) } {x:A| B'(x) } |
| def | xor
|
P XOR Q == P 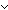 Q & Q &  (P & Q) (P & Q) |
| THM | xor_vs_neg_n_dec
|
P XOR Q   (Q (Q    P) & Dec(P) P) & Dec(P) |
| THM | exteq_subset_vs_and
|
{x:{x:A| P(x) }| Q(x) } =ext {x:A| P(x) & Q(x) } |
| THM | subset_exteq
|
( x:A. B(x) x:A. B(x)   B'(x)) B'(x))   ({x:A| B(x) } =ext {x:A| B'(x) }) ({x:A| B(x) } =ext {x:A| B'(x) }) |
| THM | subset_to_squash
|
 x:{x:A| B(x) }. x:{x:A| B(x) }. 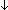 B(x) B(x) |
| THM | squash_to_subset
|
 x:A. x:A. 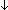 B(x) B(x)   x x  {x:A| B(x) } {x:A| B(x) } |
| THM | set_inc_wrt_imp_sq
|
( x:A. x:A. 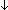 B(x) B(x)   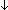 B'(x)) B'(x))   {x:A| B(x) } {x:A| B(x) } 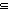 {x:A| B'(x) } {x:A| B'(x) } |
| THM | subset_sq_exteq
|
( x:A. x:A. 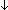 B(x) B(x)   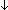 B'(x)) B'(x))   ({x:A| B(x) } =ext {x:A| B'(x) }) ({x:A| B(x) } =ext {x:A| B'(x) }) |
| THM | subset_squash_exteq
|
{x:A| 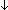 P(x) } =ext {x:A| P(x) } P(x) } =ext {x:A| P(x) } |
| THM | ifthenelse_distr_subtype
|
{x:A| if b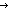 P(x) else Q(x) fi } =ext if b P(x) else Q(x) fi } =ext if b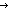 {x:A| P(x) } else {x:A| Q(x) } fi {x:A| P(x) } else {x:A| Q(x) } fi |
| def | is_discrete
|
(equality over type A is effectively decidable)
A Discrete ==  x,y:A. Dec(x = y) x,y:A. Dec(x = y) |
| THM | discrete_vs_bool
|
(A Discrete)   ( ( e:(A e:(A  A A  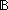 ). ).  x,y:A. (x e y) x,y:A. (x e y)   x = y) x = y) |
| THM | discrete_vs_bool2
|
(A Discrete)   ( ( e:(A e:(A  A A  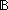 ). IsEqFun(A;e)) ). IsEqFun(A;e)) |
| def | pure_let
|
A form for function application with a special place for the argument
let x a in b(x) == b(a) a in b(x) == b(a) |
| def | pure_let2
|
let x a, y a, y b in c(x;y) == c(a;b) b in c(x;y) == c(a;b) |
| THM | no_prop_iff_its_neg
(Proof Gloss) |
No proposition is equivalent to its own negation.
 (P (P    P) P) |
| THM | RussellsParadox_Frege
|
Russell's Paradox
There is no way to represent the all properties over a class by members of the class.
 ( ( A:Type, Q:(A A:Type, Q:(A  A A  Prop). Prop).  P:(A P:(A  Prop). Prop).  p:A. p:A.  x:A. Q(x,p) x:A. Q(x,p)   P(x)) P(x)) |
| THM | RussellsParadox_Frege2
|
Russell's Paradox
Full comprehension for sets is impossible. That is, there is no notion of set such that for every property of sets there is a set consisting of the sets having that property.
 ( ( Set:Type, Set:Type,  :(Set :(Set  Set Set  Prop). Prop).
 ( ( P:(Set P:(Set  Prop). Prop).  p:Set. p:Set.  x:Set. (x x:Set. (x  p) p)   P(x)) P(x)) |
| THM | equivrel_characterization
|
A compact characterization of equivalence relations.
 R:(A R:(A  A A  Prop). Prop).
(EquivRel x,y:A. R(x,y))
 
( x:A. R(x,x) & ( x:A. R(x,x) & ( y:A. R(x,y) y:A. R(x,y)   R(y,x) & ( R(y,x) & ( z:A. R(y,z) z:A. R(y,z)   R(x,z)))) R(x,z)))) |
| def | is_the
|
(x is the unique A such that P(x))
x is the u:A. P(u) == P(x) & ( u:A. P(u) u:A. P(u)   u = x) u = x) |
| def | exists_unique
|
(there is a unique x in A such that P(x))
 !x:A. P(x) == !x:A. P(x) ==  x:A. x is the x:A. P(x) x:A. x is the x:A. P(x) |
| THM | exists_unique_elim
|
 P:(A P:(A  Prop). ( Prop). ( !u:A. P(u)) !u:A. P(u))   ( ( y,z:A. P(y) y,z:A. P(y)   P(z) P(z)   y = z) y = z) |
| THM | dec_pred_iff_some_boolfun
|
A property is effectively decidable just when it is characterized by a boolean-valued function.
( x:T. Dec(E(x))) x:T. Dec(E(x)))   ( ( f:(T f:(T  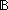 ). ).  x:T. f(x) x:T. f(x)   E(x)) E(x)) |
| THM | dec_pred_imp_bool_decider_exists
|
 P:(A P:(A  Type). ( Type). ( x:A. Dec(P(x))) x:A. Dec(P(x)))   ( ( ! ! {p:(A {p:(A  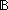 )| )|  x:A. p(x) x:A. p(x)   P(x) }) P(x) }) |
| THM | inhabited_uniquely_vs_exists_unique
|
( ! ! A) A)   ( ( !x:A. True) !x:A. True) |
| THM | indep_fun_extensional
|
Defintion of equality between functions.
 f,g:(A f,g:(A  B). f = g B). f = g   ( ( x:A. f(x) = g(x)) x:A. f(x) = g(x)) |
| THM | dep_ax_choice_version2
|
A choice principle.
( x:A. x:A.  y:B(x). Q(x,y)) y:B(x). Q(x,y))   ( ( f:(x:A f:(x:A  B(x)). B(x)).  x:A. Q(x,f(x))) x:A. Q(x,f(x))) |
| THM | fun_description
|
Existence of functions through description.
( x:A. x:A.  !y:B(x). P(x,y)) !y:B(x). P(x,y))   ( ( f:(x:A f:(x:A  B(x)). B(x)).  x:A. P(x,f(x))) x:A. P(x,f(x))) |
| THM | unique_fun_description
|
 B:(A B:(A  Type), P:(x:A Type), P:(x:A  B(x) B(x)  Prop). Prop).
( x:A. x:A.  !y:B(x). P(x,y)) !y:B(x). P(x,y))   ( ( !f:(x:A !f:(x:A  B(x)). B(x)).  x:A. P(x,f(x))) x:A. P(x,f(x))) |
| THM | unique_fun_description2
|
 B:(A B:(A  Type), P:(x:A Type), P:(x:A  B(x) B(x)  Prop). Prop).
( x:A. x:A.  !y:B(x). P(x,y)) !y:B(x). P(x,y))   ( ( ! ! {f:(x:A {f:(x:A  B(x))| B(x))|  x:A. P(x,f(x)) }) x:A. P(x,f(x)) }) |
| THM | ax_choice_version2
|
A choice principle.
( x:A. x:A.  y:B. Q(x,y)) y:B. Q(x,y))   ( ( f:(A f:(A  B). B).  x:A. Q(x,f(x))) x:A. Q(x,f(x))) |
| THM | ax_choice_version3
|
A choice principle.
( x:A. x:A.  y:B. Q(x,y)) y:B. Q(x,y))   ( ( f:(A f:(A  B). B).  x:A. Q(x,f(x))) x:A. Q(x,f(x))) |
| THM | indep_fun_description
|
( x:A. x:A.  !y:B. P(x,y)) !y:B. P(x,y))   ( ( f:(A f:(A  B). B).  x:A. P(x,f(x))) x:A. P(x,f(x))) |
| THM | unique_indep_fun_description
|
 A,B:Type{i}, P:(A A,B:Type{i}, P:(A  B B  Prop{i}). Prop{i}).
( x:A. x:A.  !y:B. P(x,y)) !y:B. P(x,y))   ( ( !f:(A !f:(A  B). B).  x:A. P(x,f(x))) x:A. P(x,f(x))) |
| THM | range_restriction_dep
|
Typing a function with its range type.
 B:(A B:(A  Type), f:(x:A Type), f:(x:A  B(x)). f B(x)). f  x:A x:A  {f(x):B(x)} {f(x):B(x)} |
| THM | range_restriction_indep
|
Typing a function with its range type.
 f:(A f:(A  B). f B). f  A A  {y:B| {y:B|  x:A. f(x) = y } x:A. f(x) = y } |
| def | diagonalize
|
Diagonalization
(Diag f wrt y. e(y))(x) == e(f(x,x)) |
| THM | diagonalization
|
 R:(B R:(B  B B  Prop), e:(B Prop), e:(B  B). B).
( b:B. b:B.  R(e(b),b)) R(e(b),b))
 
( A:Type, f:(A A:Type, f:(A  A A  B). B).  ( ( a:A. R((Diag f wrt x. e(x))(a),f(a,a)))) a:A. R((Diag f wrt x. e(x))(a),f(a,a)))) |
| THM | diagonalization_wrt_eq
|
 e:(B e:(B  B). B).
( b:B. b:B.  e(b) = b) e(b) = b)
 
( A:Type, f:(A A:Type, f:(A  A A  B). B).  ( ( a:A. (Diag f wrt x. e(x)) = f(a))) a:A. (Diag f wrt x. e(x)) = f(a))) |