| | Who Cites isect two? |
|
| isect_two | Def A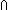 B == B == 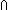 i: i: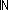 2. if i= 2. if i=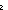 0 0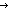 A else B fi A else B fi |
| | | Thm*  A,B:Type. A A,B:Type. A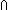 B B  Type Type |
|
| eq_int | Def i=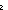 j == if i=j j == if i=j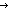 true true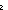 ; false ; false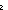 fi fi |
| | | Thm*  i,j: i,j: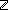 . (i= . (i=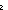 j) j)  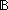 |
|
| int_seg | Def {i..j } == {k: } == {k: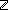 | i | i 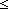 k < j } k < j } |
| | | Thm*  m,n: m,n: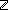 . {m..n . {m..n } }  Type Type |
|
| lelt | Def i 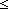 j < k == i j < k == i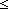 j & j<k j & j<k |
|
| le | Def A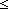 B == B ==  B<A B<A |
| | | Thm*  i,j: i,j: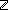 . (i . (i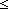 j) j)  Prop Prop |
|
| not | Def  A == A A == A   False False |
| | | Thm*  A:Prop. ( A:Prop. ( A) A)  Prop Prop |