Some definitions of interest.
sfa_doc_sexpr	Def Sexpr(A) == rec(T.(T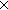T)+A)
	Thm* A:Type. Sexpr(A)  Type
sfa_doc_sexpr_cdr	Def sexprCdr(s) == Case of s :  Inj(x)  Inj(x) ; Cons(s1;s2)  s2
	Thm* A:Type, s:Sexpr(A). sexprCdr(s)  Sexpr(A)
sfa_doc_sexpr_cases	Def Case of s :  Inj(x)  g(x) ; Cons(s1;s2)  f(s1;s2) Def == InjCase(s; s1s2. s1s2/s1,s2. f(s1;s2); x. g(x))
	Thm* A:Type, C:(Sexpr(A)Type), s:Sexpr(A), Thm* f:(s1,s2:Sexpr(A)C(Cons(s1;s2))), g:(x:AC(Inj(x))). Thm* (Case of s :  Inj(x)  g(x) ; Cons(s1;s2)  f(s1,s2))  C(s)
sfa_doc_sexpr_inj	Def Inj(a) == inr(a)
	Thm* A:Type, a:A. Inj(a)  Sexpr(A)

About: IF YOU CAN SEE THIS go to /sfa/Nuprl/Shared/Xindentation_hack_doc.html