Recursive Types: rec(X.F(X))

x  A

y  A List

x.y  A List

A more general form for recursive types in Nuprl is rec(X.F(X)), where F(X) is a type-valued function of types (in X), with certain restrictions. We don't give detail on them here, but the main feature of F(X) that follows from these restrictions is that F(X) will be monotonic in type argument X, i.e.,

if A  B then F(A)  F(B), where Def S  T == x:S. x  T

For example, we could have defined a non-primitive list type as rec(X.Unit+(AX)), and interpreted inl() as the null list, and inr(<a,y>) as the list with head a  A and tail y. (See Disjoint Union, Unit and Pairs)

For the normal user, it should suffice that obviously monotonic functions on types will normally meet the criteria for forming a recursive type. (One exception is that rec(X.(X)) is does not meet the criteria stipulated for forming a type even though (X) is monotonic in X.)

A type rec(X.F(X)) is (extensionally) equal to its "unrolling" F(rec(X.F(X))), and is the smallest such type. However, unrolling rec(X.F(X)) will usually not result in an intensionally equal type. For example, rec(X.Unit+(AX)) is not intensionally equal to Unit+(Arec(X.Unit+(AX))) since they have different outermost type constructors, namely "<Type>+<Type>" and "rec([Var].<Type>)". On the other hand the type rec(X.X) does indeed unroll to itself (but Thm* Void =ext rec(A.A)).

Example: S-expressions
Here is a type definition inspired by lisp's S-expressions, which are binary trees with "atoms" at the leaves.

Def Sexpr(A) == rec(T.(TT)+A)
Def Cons(s1;s2) == inl(<s1,s2>)
Def Inj(a) == inr(a)
Def Case of s :  Inj(x)  g(x) ; Cons(s1;s2)  f(s1;s2)
Def == InjCase(s; s1s2. s1s2/s1,s2. f(s1;s2); x. g(x))

Thm* A:Type. Sexpr(A)  Type
Thm* A:Type. Sexpr(A) =ext (Sexpr(A)Sexpr(A))+A
Thm* A:Type, s1,s2:Sexpr(A). Cons(s1;s2)  Sexpr(A)
Thm* A:Type, a:A. Inj(a)  Sexpr(A)

Here is a recursive function that counts the number of leaves:

Def Size(s) == Case of s :  Inj(x)  1 ; Cons(s1;s2)  Size(s1)+Size(s2)
Def (recursive)
Thm* A:Type, s:Sexpr(A). Size(s)  

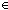
Thm* Size(Cons(Inj(1);Cons(Inj(2);Inj(1)))) = 3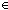  

Here is a recursive function that reverses an s-expression:

Def Reverse(e)
Def == Case of e
Def == CaInj(x)  Inj(x)
Def == CaCons(s1;s2)  Cons(Reverse(s2);Reverse(s1))
Def (recursive)
Thm* A:Type, e:Sexpr(A). Reverse(e)  Sexpr(A)

Thm* a,b,c:X.
Thm* Reverse(Cons(Inj(a);Cons(Inj(b);Inj(c))))
Thm* =
Thm* Cons(Cons(Inj(c);Inj(b));Inj(a))

Functions over recursive types are usually themselves recursive. See Recursive Functions.

About: IF YOU CAN SEE THIS go to /sfa/Nuprl/Shared/Xindentation_hack_doc.html