Recursive Functions

Def x! == if x=0 1 else x(x-1)! fi  (recursive)

where ?=? is a -valued test of integer equality.

Here's an example of how it evaluates:

3! * 3(3-1)! * 32(3-1-1)! * 321(3-1-1-1)! * 3211 * 6

Observe that execution (-1)! would never complete.

(-1)! * (-1)(-1-1)! * (-1)(-1-1)(-1-1-1)!, et cetera.

The argument that Thm* x:. x!   is carried out by induction over .
The potential and convenience of general recursion is better demonstrated with the following variant of factorial that has a result only on non-negative even inputs.

Def x! == if x=0 1 else x(x-2)! fi  (recursive)

Thm* x:{x:| (x rem 2) = 0 }. x!  

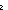
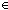
Indeed, one can even type Kleene's paradigmatic unbounded search function,

Def mu(f) == if f(0) 0 else 1+mu(x.f(1+x)) fi  (recursive)

Thm* mu  {f:()| x:. f(x) }
Thm* f:{f:()| x:. f(x) }. f(mu(f))
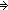
Thm* f:{f:()| x:. f(x) }, i:. i<mu(f)  f(i)

(See also Typing Y.)

One can also define type-valued functions and predicates by general recursion on the domain. Here is a definition of n-tuples defined by iterating cartesian product. We include a degenerate singleton case for 0.
Note: this is not a recursive type, but a recursive definition of a family of types. See Recursive Types.

Def A^n == if n=0 Unit ; n=1 A else A(A^(n-1)) fi  (recursive)

Thm* A:Type, n:. (A^n)  Type

Now let us compute:

A^0 * Unit
A^1 * A
A^2 * AA
A^3 * AAA

Here's a predicate on n-tuples to the effect that a tuple includes a value satisfying some property of the element type (see Propositions).

Def  u in X: A^n. P(u)
Def == n = 1   & P(X)  n2 & (X/a,rest. P(a)  ( u in rest: A^(n-1). P(u)))
Def (recursive)

Thm* A:Type, P:(AProp), n:, X:(A^n). ( u in X: A^n. P(u))  Prop

Example of use:
Thm*  i in <1,(-1),0>: ^3. i<0

About: IF YOU CAN SEE THIS go to /sfa/Nuprl/Shared/Xindentation_hack_doc.html