Reconciling Russell's "Orders" with Prop Levels

Bertrand Russell's "ramified" theory of types is the principal ancestor to intuitionistic type theory. Russell conceives of a type as a "range of significance" for a propositional function. In an impredicative logic, such as Frege's, the notion of type is "extensional" in that the type of a functional expression is determined wholly by its input and output types. For example, in Frege's logic, the types are basically these: individuals; one-place functions of individuals; one-place functions of one-place functions of individuals; two-place functions on individuals; two-place functions taking one individual and one one-place function of individuals; and so forth.

In contrast, in addition to this simple extensional type structure, there is an "intensional" aspect to Russell's types, hence the nomenclature "ramified" (meaning "branching"). Russell assigns "orders": individuals are the lowest order entities; then come propositions that don't involve quantification over propositions; then propositions that involve quantification over propositions of the previous sort; and so forth with various mixtures.

Here is Nuprl's approximation of order in ramified type theory.

In Nuprl's type theory the members of Type{1} are themselves types of individuals; call them first-order types. The members of Prop{1} are propositions involving at most quantification over first-order types of individuals; call them first-order propositions. The members of Type{2} may be totalities definable given all of Type{1} and Prop{1} themselves as classes of entities; call them second-order types (thus Type{1} and Prop{1} are second-order types). The members of Prop{2} are propositions involving at most quantification over second-order types including Type{1} and Prop{1}. And so forth.

Observe that we have included lower-order types among higher-order types, and lower-order propositions among higher-order propositions. This has a certain convenience, but is actually critical in intuitionistic computational type theory since one cannot effectively recognize when a second-order type or proposition, say, is actually first-order. For example,

Thm* f:(). (n:. if f(n)=0 False else C:Prop{1}. C fi)  Prop{2}

But whether (n:. if f(n)=0 False ; C:Prop{1}. C fi)  Prop{1} depends on whether f is everywhere zero, which is not in general recognizable.

Thm* f:(). 
Thm* (n:. f(n) = 0)
Thm*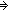 
Thm* (n:. if f(n)=0 False else C:Prop{1}. C fi)  Prop{1}

About: IF YOU CAN SEE THIS go to /sfa/Nuprl/Shared/Xindentation_hack_doc.html