Partially reflecting Howe's "squiggle" relation

This congruence relation between terms could only be directly represented in the Nuprl language itself if terms were. And while reflecting term structure is possible, it has not been implemented in the extant system. (Some theoretical work on reflection may be found in [Allen,Constable,Howe and Aitken 1987] (postscript) . Barzilay is working on newer practical methods; see [Barzilay and Allen 2002] )

However, a partial reflection of the squiggle relation between terms can be easily implemented, and exploited to allow limited reasoning about rewriting expressions in a few types that are used a lot in Nuprl. Because of this limited applicability, it is not clear how theoretically significant this partial reflection is.

The type "r ~ t" is defined semantically to be a proposition for any closed terms r and t, and is true just when the two terms are related by Howe's "squiggle" relation. One interpretation one might make is that this is equality for the type of closed terms modulo Howe's "squiggle" relation, and in the expression "r ~ t", each of r and t denotes its own equivalence class under "squiggle".

Then various rewrites can be justifed by arguments about r ~ t, such as

inferring	"1. x : H    B(x; r(x))"
from	"1. x : H    B(x; t(x))"
and	"1. x : H    r(x) ~ t(x)"

or

inferring	"1. x : H  2. B(x; r(x))    C(x)"
from	"1. x : H  2. B(x; t(x))    C(x)"
and	"1. x : H 2. B(x; r(x))   r(x) ~ t(x)".

Of course, we need to get our "r ~ t" premises from somewhere, and "  b ~ b" can get us started, but the real leverage is to exploit that for certain types commonly use in Nuprl, equal expressions in those types are always "squiggle" related. These include , , , Unit, and Atom.

Def SQType(T) == x,y:T. x = y  {x ~ y}

Thm* SQType()
Thm* SQType()
Thm* SQType()
Thm* SQType(Unit)
Thm* SQType(Atom)

But there are common types that do not have this property:

Thm* (n.n<0) = (n.false)  

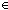
Thm* ((n.n<0) ~ (n.false))

And many ways one might chooose to represent classes of values lead to types that violate this property. For example, you might choose to represent k-tuples of numbers as {1...k}, or use "Top" rather than "Unit" as your standard 1-element type, or Top+Top instead of . You might want to define the rational numbers as equivalence classes of integer pairs rather than, say, reduced canonical fractions. In any of these scenarios the resulting types will have non-squiggle-related but equal (i.e. co-denoting) notations.

So perhaps it is best to consider the use "r ~ t" in the logic as a mere expedient.

About: IF YOU CAN SEE THIS go to /sfa/Nuprl/Shared/Xindentation_hack_doc.html