| Rank | Theorem | Name |
| 10 | Thm*  x: x: . prime(x) . prime(x) 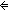  2 2 x & x &  ( ( i:{2..x i:{2..x }. i | x) }. i | x) | [prime_nat] |
| cites the following: |
| 9 | Thm*  p: p: . prime(p) . prime(p)    p = 0 & p = 0 &  (p ~ 1) & ( (p ~ 1) & ( a: a: . a | p . a | p   (a ~ 1) (a ~ 1) 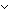 (a ~ p)) (a ~ p)) | [prime_elim] |
| 9 | Thm*  a: a: . atomic(a) . atomic(a)   prime(a) prime(a) | [atomic_imp_prime] |
| 7 | Thm*  a: a: . atomic(a) . atomic(a) 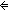   (a ~ 1) & ( (a ~ 1) & ( b: b: . b | a . b | a   (b ~ 1) (b ~ 1) 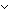 (b ~ a)) (b ~ a)) | [atomic_char] |
| 2 | Thm*  a,b: a,b: . |a| | |b| . |a| | |b| 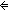  a | b a | b | [divides_of_absvals] |
| 0 | Thm*  i: i: . |i| = i . |i| = i | [absval_pos] |
| 2 | Thm* EquivRel x,y: . x ~ y . x ~ y | [assoced_equiv_rel] |
| 3 | Thm*  a: a: . |a| ~ a . |a| ~ a | [absval_assoced] |
| 6 | Thm*  a,b: a,b: . (a ~ b) . (a ~ b) 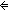  a = b a = b | [assoced_nelim] |
| 1 | Thm*  a: a: , b: , b:  . a | b . a | b   a a b b | [divisors_bound] |
| 0 | Thm*  a: a: . 0 | a . 0 | a   a = 0 a = 0 | [zero_divs_only_zero] |
| 1 | Thm* Dec(A)   ( ( (A & B) (A & B) 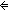   A A 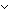  B) B) | [not_over_and] |