Selected Objects
| COM | simple_mul_factsVERSION
|
1 |
| THM | nat_prod_one_iff_factors_one
|
 x,y: x,y: . x . x y = 1 y = 1 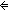  x = 1 & y = 1 x = 1 & y = 1 |
| THM | prod_zero_iff_factor_zero
|
 a,b: a,b: . a . a b = 0 b = 0 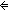  a = 0 a = 0 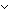 b = 0 b = 0 |
| THM | mul_nat_com
|
 a,b,c,d: a,b,c,d: . a = b . a = b   c = d c = d   a a c = d c = d b b 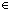  |
| THM | nat_factor_cancel_rw
|
 a,b: a,b: , n: , n:  . n . n a a n n b b 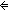  a a b b |
| THM | mul_cancel_in_eq1
|
 a,b: a,b: , n: , n:  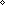 . n . n a = n a = n b b 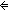  a = b a = b |
| THM | mul_cancel_in_eq2
|
 a,b: a,b: , m,n: , m,n:  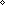 . m = n . m = n   (m (m a = n a = n b b 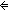  a = b) a = b) |
| THM | le_mul_rt_by_pos
|
 x,y: x,y: , z: , z:  . x . x y y   x x y y z z |
| THM | factor_bound
|
 k: k:  , n: , n: , x,y: , x,y: . k . k x+n = k x+n = k y y   x x y y |
| THM | lt_mul_rt_by_pos
|
 x,y: x,y: , z: , z:  . x<y . x<y   x<y x<y z z |
| THM | factors_bound
|
 i,j: i,j:  . i . i i i j & j j & j i i j j |
| THM | pos_mul_arg_boundsNat
|
 a,b: a,b: . 0<a . 0<a b b 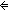  0<a & 0<b 0<a & 0<b |
| THM | pos_mul_arg_boundsNat2
|
 i,j: i,j: . 0<i . 0<i j j   i i i i j & j j & j i i j j |
| THM | factor_smaller
|
 i:{2...}, j:{1...}. j<i i:{2...}, j:{1...}. j<i j j |
| THM | factor_smaller2
|
 i:{2...}, j: i:{2...}, j:  . j<i . j<i j j |
| THM | factors_smaller
|
 i,j:{2...}. i<i i,j:{2...}. i<i j & j<i j & j<i j j |
| THM | factors_smaller2
|
 k: k:  , i:{2..k , i:{2..k }, j: }, j: . i . i j = k j = k   2 2  j < k & i<k j < k & i<k |
| THM | mul_nat_plus
|
 x,y: x,y:  . x . x y y 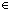   |
| THM | divides_def_on_nat
|
a divides b (specialized to natural numbers)
 a,b: a,b: . a | b . a | b 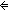  ( ( c: c: . b = a . b = a c) c) |
| THM | only_one_nat_divs_one
|
 b: b: . b | 1 . b | 1   b = 1 b = 1 |
| THM | div_inverts_nat_mul
|
 x,y: x,y: , z: , z:  . x = y . x = y z z   (x (x  z) = y z) = y |
| THM | div_inverts_nat_mul2
|
 x: x:  , y,z: , y,z: . x = y . x = y z z   (x (x  z) = y z) = y |
| THM | prime_nat
|
 x: x: . prime(x) . prime(x) 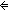  2 2 x & x &  ( ( i:{2..x i:{2..x }. i | x) }. i | x) |
| def | prime_nats
|
Prime == {x: == {x: | prime(x) } | prime(x) } |
| THM | natprimes_lb
|
 x: x: . prime(x) . prime(x)   2 2 x x |
| THM | natprime_nondivs
|
 x: x: . prime(x) . prime(x)   ( ( i:{2..x i:{2..x }. }.  i | x) i | x) |
| THM | nonprime_nat
|
 x: x: . .  prime(x) prime(x) 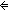  x<2 x<2 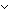 ( ( i,j:{2..x i,j:{2..x }. x = i }. x = i j) j) |
| THM | composite_with_prime_factor
|
 x:{2...}. x:{2...}.  prime(x) prime(x)   ( ( i,j:{2..x i,j:{2..x }. x = i }. x = i j & prime(i)) j & prime(i)) |
| THM | prime_or_smaller_prime_factor2
|
 x:{2...}. x:{2...}.  p:{2...}, c:{1...}. p p:{2...}, c:{1...}. p x & prime(p) & x = p x & prime(p) & x = p c c |
| THM | prime_or_smaller_prime_factor
|
A number bigger than 1 is divisible by a prime.
 x:{2...}. x:{2...}.  p:{2...}. p p:{2...}. p x & prime(p) & p | x x & prime(p) & p | x |
| THM | prime_neg
|
 y: y: . prime(-y) . prime(-y) 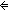  prime(y) prime(y) |
| THM | decidable__prime
|
 x: x: . Dec(prime(x)) . Dec(prime(x)) |
| THM | prime_decider_exists
|
 ! !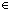 {p:( {p:(   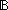 )| )|  x: x: . p(x) . p(x) 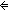  prime(x) } prime(x) } |
| def | prime_decider
|
Boolean decider for primeness implicit in Thm*  ! !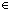 {p:( {p:(   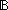 )| )|  x: x: . p(x) . p(x) 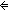  prime(x) } prime(x) }
is_prime(x) == prime_decider_exists{1:l}(x) |
| THM | no_nat_prime_divs_one
|
 b: b: . b | 1 . b | 1    prime(b) prime(b) |
| THM | no_prime_divs_one
|
One has no prime divisors.
 b: b: . b | 1 . b | 1    prime(b) prime(b) |
| THM | no_prime_divs_one_b
|
One has no prime divisors.
 b: b: . prime(b) . prime(b)    b | 1 b | 1 |
| THM | prime_nat_divby_self_only
|
 x:{2...}, y: x:{2...}, y: . prime(y) . prime(y)   x | y x | y   x = y x = y 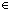  |
| THM | prime_among_factors
|
Factoring a prime always includes the prime itself.
 a,b: a,b: . prime(a . prime(a b) b)   a a b = a b = a 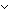 a a b = b b = b |