| | Who Cites equiv rel? |
|
| equiv_rel | Def EquivRel x,y:T. E(x;y)
Def == Refl(T;x,y.E(x;y)) & (Sym x,y:T. E(x;y)) & (Trans x,y:T. E(x;y)) |
| | | Thm*  T:Type, E:(T T:Type, E:(T  T T  Prop). (EquivRel x,y:T. E(x,y)) Prop). (EquivRel x,y:T. E(x,y)) 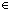 Prop Prop |
|
| trans | Def Trans x,y:T. E(x;y) ==  a,b,c:T. E(a;b) a,b,c:T. E(a;b)   E(b;c) E(b;c)   E(a;c) E(a;c) |
| | | Thm*  T:Type, E:(T T:Type, E:(T  T T  Prop). (Trans x,y:T. E(x,y)) Prop). (Trans x,y:T. E(x,y)) 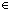 Prop Prop |
|
| sym | Def Sym x,y:T. E(x;y) ==  a,b:T. E(a;b) a,b:T. E(a;b)   E(b;a) E(b;a) |
| | | Thm*  T:Type, E:(T T:Type, E:(T  T T  Prop). (Sym x,y:T. E(x,y)) Prop). (Sym x,y:T. E(x,y)) 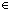 Prop Prop |
|
| refl | Def Refl(T;x,y.E(x;y)) ==  a:T. E(a;a) a:T. E(a;a) |
| | | Thm*  T:Type, E:(T T:Type, E:(T  T T  Prop). Refl(T;x,y.E(x,y)) Prop). Refl(T;x,y.E(x,y)) 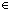 Prop Prop |