Selected Objects
| Introduction | Introductory Remarks |
| def | bool |
 == Unit+Unit == Unit+Unit |
| def | btrue |
true == inl( == inl(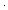 ) ) |
| def | bfalse |
false == inr( == inr(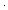 ) ) |
| def | ifthenelse |
if b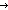 t else f fi == InjCase(b ; t; f) t else f fi == InjCase(b ; t; f) |
| def | assert |
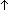 b == if b b == if b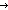 True else False fi True else False fi |
| def | b2i |
b2i(b) == if b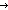 1 else 0 fi 1 else 0 fi |
| THM | b2i_bounds |
 b: b: . 0 . 0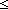 b2i(b) & b2i(b) b2i(b) & b2i(b)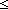 1 1 |
| def | bnot |
  b == if b b == if b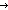 false false else true else true fi fi |
| def | band |
p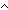  q == if p q == if p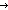 q else false q else false fi fi |
| def | bor |
p 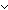  q == if p q == if p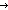 true true else q fi else q fi |
| def | eq_bool |
p= q == (p q == (p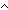  q) q) 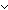  ( (  p p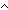    q) q) |
| def | bxor |
p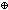  q == (p q == (p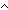    q) q) 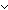  ( (  p p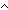  q) q) |
| def | bimplies |
p   q == q ==   p p 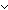  q q |
| def | rev_bimplies |
p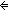   q == q q == q   p p |
| def | eq_int |
i= j == if i=j j == if i=j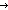 true true ; false ; false fi fi |
| def | lt_int |
i< j == if i<j j == if i<j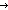 true true ; false ; false fi fi |
| def | eq_atom |
x= y y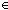 Atom == if x=y Atom == if x=y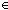 Atom Atom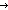 true true ; false ; false fi fi |
| def | le_int |
i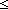  j == j ==   j< j< i i |
| COM | bool_thms |
================GENERAL THEOREMS================ |
| THM | btrue_neq_bfalse |
 true true = false = false |
| THM | bool_cases |
 b: b: . b = true . b = true 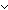 b = false b = false |
| THM | bool_ind |
 P:( P:(  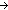 Prop). P(false Prop). P(false ) )   P(true P(true ) )   ( ( b: b: . P(b)) . P(b)) |
| THM | decidable__equal_bool |
 a,b: a,b: . Dec(a = b) . Dec(a = b) |
| THM | bnot_bnot_elim |
 p: p: . .     p = p p = p |
| THM | bnot_thru_band |
 p,q: p,q: . .   (p (p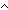  q) = ( q) = (  p p 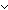    q) q) |
| THM | bnot_thru_bor |
 p,q: p,q: . .   (p (p 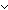  q) = ( q) = (  p p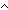    q) q) |
| THM | bnot_of_le_int |
 i,j: i,j: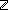 . .   i i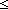  j = (j< j = (j< i) i) |
| THM | bimplies_weakening |
 u,v: u,v: . u = v . u = v   u u   v v |
| THM | bimplies_transitivity |
 u,v,w: u,v,w: . u . u   v v   v v   w w   u u   w w |
| THM | assert_functionality_wrt_bimplies |
 u,v: u,v: . u . u   v v   u u   v v |
| COM | bool_simp_1 |
CONSTANT SIMPLIFICATION
... |
| THM | bor_ff_simp |
 u: u: . (u . (u 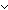  false false ) = u ) = u |
| THM | bor_tt_simp |
 u: u: . (u . (u 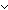  true true ) = true ) = true |
| THM | band_ff_simp |
 u: u: . (u . (u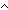  false false ) = false ) = false |
| THM | band_tt_simp |
 u: u: . (u . (u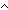  true true ) = u ) = u |
| COM | assert_com |
`ASSERT'-RELATED THEOREMS |
| THM | assert_of_tt |
true |
| THM | assert_of_ff |
 false false |
| THM | assert_elim |
 b: b: . b . b   b = true b = true |
| THM | not_assert_elim |
 b: b: . .  b b   b = false b = false |
| THM | eqtt_to_assert |
 b: b: . b = true . b = true 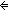  b b |
| THM | eqff_to_assert |
 b: b: . b = false . b = false 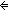    b b |
| THM | decidable__assert |
 b: b: . Dec(b) . Dec(b) |
| THM | iff_imp_equal_bool |
 a,b: a,b: . (a . (a 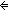  b) b)   a = b a = b |
| THM | assert_of_eq_atom |
 x,y:Atom. x= x,y:Atom. x= y y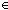 Atom Atom 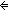  x = y x = y |
| THM | assert_of_eq_int |
 x,y: x,y: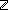 . x= . x= y y 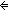  x = y x = y |
| THM | neg_assert_of_eq_int |
 x,y: x,y: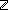 . .  x= x= y y 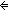  x x 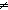 y y |
| THM | neg_assert_of_eq_atom |
 x,y:Atom. x,y:Atom.  x= x= y y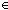 Atom Atom 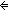  x x 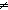 y y |
| THM | assert_of_lt_int |
 x,y: x,y: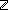 . x< . x< y y 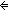  x<y x<y |
| THM | assert_of_eq_int_rw |
 x,y: x,y: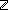 . x= . x= y y 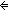  x = y x = y |
| THM | assert_of_eq_bool |
 p,q: p,q: . p= . p= q q 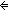  p = q p = q |
| THM | assert_of_bnot |
 p: p: . .   p p 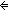   p p |
| THM | assert_of_band |
 p,q: p,q: . (p . (p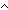  q) q) 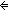  p & q p & q |
| THM | assert_of_bor |
 p,q: p,q: . (p . (p 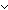  q) q) 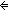  p p 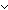 q q |
| THM | assert_of_bimplies |
 p,q: p,q: . p . p   q q 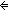  (p (p   q) q) |
| THM | assert_of_le_int |
 x,y: x,y: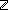 . x . x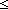  y y 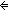  x x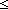 y y |
| THM | ite_rw_test |
 n: n: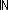 , i:{1..n , i:{1..n }. }.  0 = 0 & 0 = 0 &  n = 0 n = 0   False False |
| THM | ite_rw_false |
 b: b: , x,y:T. , x,y:T.  b b   if b if b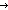 x else y fi = y x else y fi = y |
| THM | ite_rw_true |
 b: b: , x,y:T. b , x,y:T. b   if b if b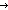 x else y fi = x x else y fi = x |
| THM | fun_thru_ite |
 f:(S f:(S 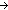 T), b: T), b: , p,q:S. f(if b , p,q:S. f(if b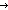 p else q fi) = if b p else q fi) = if b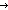 f(p) else f(q) fi f(p) else f(q) fi |
| COM | old_bool_1_stuff |
OLD STUFF
... |
| THM | eq_int_eq_false |
 i,j: i,j: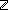 . i . i 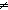 j j   (i= (i= j) = false j) = false |
| THM | eq_int_eq_true |
 i,j: i,j: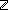 . i = j . i = j   (i= (i= j) = true j) = true |
| THM | eq_int_eq_false_elim |
 i,j: i,j: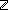 . (i= . (i= j) = false j) = false   i i 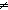 j j |
| THM | eq_int_eq_true_elim |
 i,j: i,j: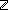 . (i= . (i= j) = true j) = true   i = j i = j |
| THM | eq_int_cases_test |
 x,y:A, P:(A x,y:A, P:(A 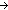 Prop), i,j: Prop), i,j: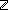 . P(if i= . P(if i= j j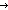 x else y fi) x else y fi)   P(if i= P(if i= j j x else y fi) x else y fi) |