Thm*  a:T, Q:(T a:T, Q:(T  Prop). (a = !x:T. Q(x)) Prop). (a = !x:T. Q(x))   a a 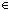 {!x:T | Q(x)} {!x:T | Q(x)} | [uni_sat_imp_in_uni_set] |
Thm*  a:T, x:{a:T}. x = a a:T, x:{a:T}. x = a 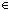 T T | [singleton_properties] |
Thm*  B:(A B:(A  Type), p:(x:A Type), p:(x:A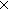 B(x)), C:Type, b:(x:A B(x)), C:Type, b:(x:A  B(x) B(x)  C). C).
Thm* (p/x,y. b(x,y)) = b(1of(p),2of(p)) | [spread_to_pi12] |
Thm*  B:(A B:(A  Type), p:(x:A Type), p:(x:A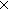 B(x)), C,D:Type, f:(C B(x)), C,D:Type, f:(C  D), b:(x:A D), b:(x:A  B(x) B(x)  C). C).
Thm* f(p/x,y. b(x,y)) = (p/x,y. f(b(x,y))) | [fun_thru_spread] |
Thm*  A,B:Type, a:A, b:(A A,B:Type, a:A, b:(A  B). let x = a in b(x) B). let x = a in b(x) 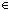 B B | [let_wf] |
Thm* (P   Q) Q)   (Q (Q   P) P)   (P (P   Q) Q) | [implies_antisymmetry] |
Thm* (P   Q) Q)   ( (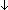 P P   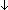 Q) Q) | [squash_functionality_wrt_iff] |
Thm* (P   Q) Q)   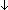 P P   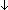 Q Q | [squash_functionality_wrt_implies] |
Thm* (P1   P2) P2)   (Q1 (Q1   Q2) Q2)   P1 P1  Q1 Q1   P2 P2  Q2 Q2 | [or_functionality_wrt_implies] |
Thm* (P1   P2) P2)   (Q1 (Q1   Q2) Q2)   (P1 (P1  Q1 Q1   P2 P2  Q2) Q2) | [or_functionality_wrt_iff] |
Thm* (P   Q) Q)    P P    Q Q | [not_functionality_wrt_implies] |
Thm* (P   Q) Q)   ( ( P P    Q) Q) | [not_functionality_wrt_iff] |
Thm*  P,Q:(S P,Q:(S  Prop). Prop).
Thm* S = T   ( ( x:S. P(x) x:S. P(x)   Q(x)) Q(x))   ( (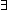 x:S. P(x)) x:S. P(x))   ( (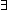 y:T. Q(y)) y:T. Q(y)) | [exists_functionality_wrt_implies] |
Thm*  P,Q:(S P,Q:(S  Prop). Prop).
Thm* S = T   ( ( x:S. P(x) x:S. P(x)   Q(x)) Q(x))   (( ((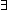 x:S. P(x)) x:S. P(x))   ( (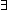 y:T. Q(y))) y:T. Q(y))) | [exists_functionality_wrt_iff] |
Thm*  P,Q:(S P,Q:(S  Prop). Prop).
Thm* S = T   ( ( z:S. P(z) z:S. P(z)   Q(z)) Q(z))   ( ( x:S. P(x)) x:S. P(x))   ( ( y:T. Q(y)) y:T. Q(y)) | [all_functionality_wrt_implies] |
Thm*  P,Q:(S P,Q:(S  Prop). Prop).
Thm* S = T   ( ( x:S. P(x) x:S. P(x)   Q(x)) Q(x))   (( (( x:S. P(x)) x:S. P(x))   ( ( y:T. Q(y))) y:T. Q(y))) | [all_functionality_wrt_iff] |
Thm* (P1   P2) P2)   (Q1 (Q1   Q2) Q2)   ((P1 ((P1   Q1) Q1)   (P2 (P2   Q2)) Q2)) | [iff_functionality_wrt_iff] |
Thm* (P   Q) Q)   (Dec(P) (Dec(P)   Dec(Q)) Dec(Q)) | [decidable_functionality] |
Thm* (P1   P2) P2)   (Q1 (Q1   Q2) Q2)   (P1 (P1   Q1) Q1)   P2 P2   Q2 Q2 | [implies_functionality_wrt_implies] |
Thm* (P1   P2) P2)   (Q1 (Q1   Q2) Q2)   ((P1 ((P1   Q1) Q1)   (P2 (P2   Q2)) Q2)) | [implies_functionality_wrt_iff] |
Thm* (P1   P2) P2)   (Q1 (Q1   Q2) Q2)   P1 & Q1 P1 & Q1   P2 & Q2 P2 & Q2 | [and_functionality_wrt_implies] |
Thm* (P1   P2) P2)   (Q1 (Q1   Q2) Q2)   (P1 & Q1 (P1 & Q1   P2 & Q2) P2 & Q2) | [and_functionality_wrt_iff] |
Thm* (P   Q) Q)   (Q (Q   R) R)   P P   R R | [implies_transitivity] |
Thm* (P   Q) Q)   (Q (Q   R) R)   (P (P   R) R) | [iff_transitivity] |
Thm*  Q:(T Q:(T  Prop). Prop).  ( (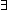 x:T. Q(x)) x:T. Q(x))   ( ( x:T. x:T.  Q(x)) Q(x)) | [not_over_exists] |
Thm*  B:(T B:(T  Prop). ( Prop). (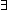 x:T. A & B(x)) x:T. A & B(x))   A & ( A & (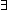 x:T. B(x)) x:T. B(x)) | [exists_over_and_r] |
Thm* A  True True   True True | [or_true_r] |
Thm* True  A A   True True | [or_true_l] |
Thm* A  False False   A A | [or_false_r] |
Thm* False  A A   A A | [or_false_l] |
Thm* A & True   A A | [and_true_r] |
Thm* True & A   A A | [and_true_l] |
Thm* A & False   False False | [and_false_r] |
Thm* False & A   False False | [and_false_l] |
Thm* Dec(A)   ( ( (A & B) (A & B)    A A   B) B) | [not_over_and] |
Thm*  A A   B B    (A & B) (A & B) | [not_over_and_b] |
Thm*  (A (A  B) B)    A & A &  B B | [not_over_or_a] |
Thm*  (A (A  B) B)    A & A &  B B | [not_over_or] |
Thm* A  B B   B B  A A | [or_comm] |
Thm* A  (B (B  C) C)   (A (A  B) B)  C C | [or_assoc] |
Thm* A & B   B & A B & A | [and_comm] |
Thm* A & (B & C)   (A & B) & C (A & B) & C | [and_assoc] |
Thm* (A   B) B)   (B (B   A) A) | [iff_symmetry] |
Thm* Dec(A)   ( (  A A   A) A) | [dneg_elim_a] |
Thm* Dec(A)     A A   A A | [dneg_elim] |
Thm* SqStable(P)   ( (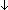 P P   P) P) | [squash_elim] |
Thm* Dec(P)   SqStable(P) SqStable(P) | [sq_stable_from_decidable] |
Thm* SqStable( P) P) | [sq_stable__not] |
Thm* Stable{P}   SqStable(P) SqStable(P) | [sq_stable__from_stable] |
Thm* SqStable(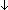 P) P) | [sq_stable__squash] |
Thm*  x,y:A. SqStable(x = y) x,y:A. SqStable(x = y) | [sq_stable__equal] |
Thm*  P:(A P:(A  Prop). ( Prop). ( x:A. SqStable(P(x))) x:A. SqStable(P(x)))   SqStable( SqStable( x:A. P(x)) x:A. P(x)) | [sq_stable__all] |
Thm* SqStable(P)   SqStable(Q) SqStable(Q)   SqStable(P SqStable(P   Q) Q) | [sq_stable__iff] |
Thm* SqStable(Q)   SqStable(P SqStable(P   Q) Q) | [sq_stable__implies] |
Thm* SqStable(P)   SqStable(Q) SqStable(Q)   SqStable(P & Q) SqStable(P & Q) | [sq_stable__and] |
Thm* Dec(P)   Stable{P} Stable{P} | [stable__from_decidable] |
Thm*  f,g:(A f,g:(A  B). ( B). ( x:A. Stable{f(x) = g(x)}) x:A. Stable{f(x) = g(x)})   Stable{f = g} Stable{f = g} | [stable__function_equal] |
Thm* Stable{ P} P} | [stable__not] |
Thm* Dec(A)   (A (A   B) B)   Dec(B) Dec(B) | [iff_preserves_decidability] |
Thm*  a,b:Atom. Dec(a = b) a,b:Atom. Dec(a = b) | [decidable__atom_equal] |
Thm*  i,j: i,j: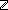 . Dec(i = j) . Dec(i = j) | [decidable__int_equal] |
Thm* Dec(P)   Dec(Q) Dec(Q)   Dec(P Dec(P   Q) Q) | [decidable__iff] |
Thm* Dec(P)   Dec(Q) Dec(Q)   Dec(P Dec(P   Q) Q) | [decidable__implies] |
Thm* Dec(P)   Dec(Q) Dec(Q)   Dec(P & Q) Dec(P & Q) | [decidable__and] |
Thm* Dec(P)   Dec(Q) Dec(Q)   Dec(P Dec(P  Q) Q) | [decidable__or] |
Thm*  a:Unit. a = a:Unit. a = 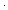 | [unit_triviality] |
Thm*  B:(A B:(A  Type), p:(a:A Type), p:(a:A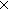 B(a)). <1of(p),2of(p)> = p B(a)). <1of(p),2of(p)> = p 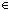 a:A a:A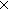 B(a) B(a) | [pair_eta_rw] |
Thm*  A:Type, B:(A A:Type, B:(A  Type), p:(a:A Type), p:(a:A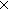 B(a)). 2of(p) B(a)). 2of(p) 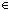 B(1of(p)) B(1of(p)) | [pi2_wf] |
Thm*  A:Type, a:A. (a A:Type, a:A. (a 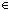 A) A) 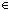 Type Type | [member_wf] |
Def a = !x:T. Q(x) == Q(a) & ( a':T. Q(a') a':T. Q(a')   a' = a) a' = a) | [uni_sat] |
Def {!x:T | P(x)} == {x:T| P(x) & ( y:T. P(y) y:T. P(y)   y = x) } y = x) } | [unique_set] |
Def XM ==  P:Prop. Dec(P) P:Prop. Dec(P) | [xmiddle] |
Def S 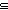 T == T ==  x:S. x x:S. x 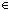 T T | [subtype] |