Selected Objects
| def | unit |
Unit == 0 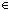 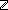 |
| def | true |
True == 0 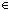 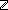 |
| def | false |
False == Void |
| def | and |
P & Q == P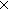 Q Q |
| def | or |
P  Q == P+Q Q == P+Q |
| def | implies |
P   Q == P Q == P  Q Q |
| def | rev_implies |
P   Q == Q Q == Q   P P |
| def | squash |
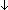 T == {:True| T } T == {:True| T } |
| def | not |
 A == A A == A   False False |
| def | nequal |
a 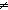 b b 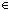 T == T ==  a = b a = b 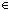 T T |
| def | iff |
P   Q == (P Q == (P   Q) & (P Q) & (P   Q) Q) |
| def | exists |
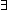 x:A. B(x) == x:A x:A. B(x) == x:A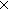 B(x) B(x) |
| def | sq_exists |
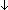 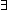 x:A. B(x) == {x:A| B(x) } x:A. B(x) == {x:A| B(x) } |
| def | all |
 x:A. B(x) == x:A x:A. B(x) == x:A  B(x) B(x) |
| def | le |
A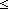 B == B ==  B<A B<A |
| def | ge |
i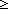 j == j j == j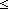 i i |
| def | gt |
i>j == j<i |
| def | subtype |
S 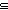 T == T ==  x:S. x x:S. x 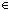 T T |
| def | top |
Top == Void(given Void) |
| COM | core_2_summary |
General-purpose definitions andtheorems. |
| COM | core_2_intro |
Introduces a variety of general-purpose definitions andtheorems. |
| def | infix_ap |
x f y == f(x,y) |
| def | label |
t ...$L == t |
| def | guard |
{T} == T |
| def | error |
??? == "error" |
| def | prop |
Prop == Type |
| def | cand |
A & B == A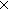 B B |
| COM | COMBS_acom |
Common Combinators |
| def | icomb |
I(x) == x |
| def | kcomb |
K(x,y) == x |
| def | scomb |
S(x,y,z) == x(z,y(z)) |
| COM | PRODUCT_DEFS_acom |
Projection functions for pairs |
| def | pi1 |
1of(t) == t.1 |
| def | pi2 |
2of(t) == t.2 |
| THM | pair_eta_rw |
 B:(A B:(A  Type), p:(a:A Type), p:(a:A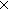 B(a)). <1of(p),2of(p)> = p B(a)). <1of(p),2of(p)> = p 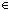 a:A a:A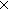 B(a) B(a) |
| def | spread3 |
let x,y,z = a in t(x;y;z) == a/x,zz. zz/y,z. t(x;y;z) |
| def | spread4 |
let w,x,y,z = a in t(w;x;y;z) == a/w,zz1. zz1/x,zz2. zz2/y,z. t(w;x;y;z) |
| def | spread5 |
let a,b,c,d,e = u in v(a;b;c;d;e)
== u/a,zz1. zz1/b,zz2. zz2/c,zz3. zz3/d,e. v(a;b;c;d;e) |
| def | spread6 |
let a,b,c,d,e,f = u in v(a;b;c;d;e;f)
== u/a,zz1. zz1/b,zz2. zz2/c,zz3. zz3/d,zz4. zz4/e,f. v(a;b;c;d;e;f) |
| def | spread7 |
let a,b,c,d,e,f,g = u in v(a;b;c;d;e;f;g)
== u/a,zz1.
== zz1/b,zz2. zz2/c,zz3. zz3/d,zz4. zz4/e,zz5. zz5/f,g. v(a;b;c;d;e;f;g) |
| COM | UNIT_DEFS_acom |
Inhabitant of Unit type |
| def | it |
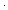 == * == * |
| THM | unit_triviality |
 a:Unit. a = a:Unit. a = 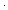 |
| COM | CONSTR_PROPERTIES_com |
Predicates for constructive properties of propositions, andlemmas characterizing how these predicates are inherited.Worthwhile sometime redoing thms for soft abstractionsin terms of the underlying hard abstractions / primitives. |
| def | decidable |
Dec(P) == P   P P |
| THM | decidable__or |
Dec(P)   Dec(Q) Dec(Q)   Dec(P Dec(P  Q) Q) |
| THM | decidable__and |
Dec(P)   Dec(Q) Dec(Q)   Dec(P & Q) Dec(P & Q) |
| THM | decidable__implies |
Dec(P)   Dec(Q) Dec(Q)   Dec(P Dec(P   Q) Q) |
| THM | decidable__false |
Dec(False) |
| THM | decidable__iff |
Dec(P)   Dec(Q) Dec(Q)   Dec(P Dec(P   Q) Q) |
| THM | decidable__int_equal |
 i,j: i,j: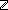 . Dec(i = j) . Dec(i = j) |
| THM | decidable__atom_equal |
 a,b:Atom. Dec(a = b) a,b:Atom. Dec(a = b) |
| THM | iff_preserves_decidability |
Dec(A)   (A (A   B) B)   Dec(B) Dec(B) |
| def | stable |
Stable{P} ==   P P   P P |
| THM | stable__not |
Stable{ P} P} |
| THM | stable__function_equal |
 f,g:(A f,g:(A  B). ( B). ( x:A. Stable{f(x) = g(x)}) x:A. Stable{f(x) = g(x)})   Stable{f = g} Stable{f = g} |
| THM | stable__from_decidable |
Dec(P)   Stable{P} Stable{P} |
| def | sq_stable |
SqStable(P) == 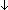 P P   P P |
| THM | sq_stable__and |
SqStable(P)   SqStable(Q) SqStable(Q)   SqStable(P & Q) SqStable(P & Q) |
| THM | sq_stable__implies |
SqStable(Q)   SqStable(P SqStable(P   Q) Q) |
| THM | sq_stable__iff |
SqStable(P)   SqStable(Q) SqStable(Q)   SqStable(P SqStable(P   Q) Q) |
| THM | sq_stable__all |
 P:(A P:(A  Prop). ( Prop). ( x:A. SqStable(P(x))) x:A. SqStable(P(x)))   SqStable( SqStable( x:A. P(x)) x:A. P(x)) |
| THM | sq_stable__equal |
 x,y:A. SqStable(x = y) x,y:A. SqStable(x = y) |
| THM | sq_stable__squash |
SqStable(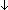 P) P) |
| THM | sq_stable__from_stable |
Stable{P}   SqStable(P) SqStable(P) |
| THM | sq_stable__not |
SqStable( P) P) |
| THM | sq_stable_from_decidable |
Dec(P)   SqStable(P) SqStable(P) |
| def | xmiddle |
XM ==  P:Prop. Dec(P) P:Prop. Dec(P) |
| THM | squash_elim |
SqStable(P)   ( (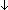 P P   P) P) |
| COM | LOGIC_THMS_tcom |
Theorems of inituitionistic propositional and predicate logic. |
| THM | dneg_elim |
Dec(A)     A A   A A |
| THM | dneg_elim_a |
Dec(A)   ( (  A A   A) A) |
| THM | iff_symmetry |
(A   B) B)   (B (B   A) A) |
| THM | and_assoc |
A & (B & C)   (A & B) & C (A & B) & C |
| THM | and_comm |
A & B   B & A B & A |
| THM | or_assoc |
A  (B (B  C) C)   (A (A  B) B)  C C |
| THM | or_comm |
A  B B   B B  A A |
| THM | not_over_or |
 (A (A  B) B)    A & A &  B B |
| THM | not_over_or_a |
 (A (A  B) B)    A & A &  B B |
| THM | not_over_and_b |
 A A   B B    (A & B) (A & B) |
| THM | not_over_and |
Dec(A)   ( ( (A & B) (A & B)    A A   B) B) |
| THM | and_false_l |
False & A   False False |
| THM | and_false_r |
A & False   False False |
| THM | and_true_l |
True & A   A A |
| THM | and_true_r |
A & True   A A |
| THM | or_false_l |
False  A A   A A |
| THM | or_false_r |
A  False False   A A |
| THM | or_true_l |
True  A A   True True |
| THM | or_true_r |
A  True True   True True |
| THM | exists_over_and_r |
 B:(T B:(T  Prop). ( Prop). (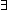 x:T. A & B(x)) x:T. A & B(x))   A & ( A & (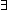 x:T. B(x)) x:T. B(x)) |
| THM | not_over_exists |
 Q:(T Q:(T  Prop). Prop).  ( (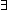 x:T. Q(x)) x:T. Q(x))   ( ( x:T. x:T.  Q(x)) Q(x)) |
| COM | EQUALITY_THMS_tcom |
Equality Theorems |
| COM | REWRITE_SUPPORT_tcom |
Lemma support for rewriting. |
| THM | iff_transitivity |
(P   Q) Q)   (Q (Q   R) R)   (P (P   R) R) |
| THM | implies_transitivity |
(P   Q) Q)   (Q (Q   R) R)   P P   R R |
| THM | and_functionality_wrt_iff |
(P1   P2) P2)   (Q1 (Q1   Q2) Q2)   (P1 & Q1 (P1 & Q1   P2 & Q2) P2 & Q2) |
| THM | and_functionality_wrt_implies |
(P1   P2) P2)   (Q1 (Q1   Q2) Q2)   P1 & Q1 P1 & Q1   P2 & Q2 P2 & Q2 |
| THM | implies_functionality_wrt_iff |
(P1   P2) P2)   (Q1 (Q1   Q2) Q2)   ((P1 ((P1   Q1) Q1)   (P2 (P2   Q2)) Q2)) |
| THM | implies_functionality_wrt_implies |
(P1   P2) P2)   (Q1 (Q1   Q2) Q2)   (P1 (P1   Q1) Q1)   P2 P2   Q2 Q2 |
| THM | decidable_functionality |
(P   Q) Q)   (Dec(P) (Dec(P)   Dec(Q)) Dec(Q)) |
| THM | iff_functionality_wrt_iff |
(P1   P2) P2)   (Q1 (Q1   Q2) Q2)   ((P1 ((P1   Q1) Q1)   (P2 (P2   Q2)) Q2)) |
| THM | all_functionality_wrt_iff |
 P,Q:(S P,Q:(S  Prop). S = T Prop). S = T   ( ( x:S. P(x) x:S. P(x)   Q(x)) Q(x))   (( (( x:S. P(x)) x:S. P(x))   ( ( y:T. Q(y))) y:T. Q(y))) |
| THM | all_functionality_wrt_implies |
 P,Q:(S P,Q:(S  Prop). S = T Prop). S = T   ( ( z:S. P(z) z:S. P(z)   Q(z)) Q(z))   ( ( x:S. P(x)) x:S. P(x))   ( ( y:T. Q(y)) y:T. Q(y)) |
| THM | exists_functionality_wrt_iff |
 P,Q:(S P,Q:(S  Prop). S = T Prop). S = T   ( ( x:S. P(x) x:S. P(x)   Q(x)) Q(x))   (( ((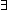 x:S. P(x)) x:S. P(x))   ( (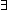 y:T. Q(y))) y:T. Q(y))) |
| THM | exists_functionality_wrt_implies |
 P,Q:(S P,Q:(S  Prop). S = T Prop). S = T   ( ( x:S. P(x) x:S. P(x)   Q(x)) Q(x))   ( (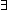 x:S. P(x)) x:S. P(x))   ( (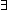 y:T. Q(y)) y:T. Q(y)) |
| THM | not_functionality_wrt_iff |
(P   Q) Q)   ( ( P P    Q) Q) |
| THM | not_functionality_wrt_implies |
(P   Q) Q)    P P    Q Q |
| THM | or_functionality_wrt_iff |
(P1   P2) P2)   (Q1 (Q1   Q2) Q2)   (P1 (P1  Q1 Q1   P2 P2  Q2) Q2) |
| THM | or_functionality_wrt_implies |
(P1   P2) P2)   (Q1 (Q1   Q2) Q2)   P1 P1  Q1 Q1   P2 P2  Q2 Q2 |
| THM | squash_functionality_wrt_implies |
(P   Q) Q)   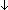 P P   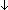 Q Q |
| THM | squash_functionality_wrt_iff |
(P   Q) Q)   ( (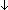 P P   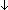 Q) Q) |
| THM | implies_antisymmetry |
(P   Q) Q)   (Q (Q   P) P)   (P (P   Q) Q) |
| COM | MISC_DEFS_com |
Miscellaneous General Definitions |
| def | let |
let x = a in b(x) == (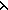 x.b(x))(a) x.b(x))(a) |
| COM | type_inj_acom |
type_inj is intended chiefly for injecting into quotienttypes. For convenience, typing lemmas should be provenfor each application. e.g. ...  x:T. [x]{a,b:T//Eab}A general typing lemma for type_inj(x;T) cannotbe proven, because it's antecedent would involve the subtypepredicate which isn't typeable. x:T. [x]{a,b:T//Eab}A general typing lemma for type_inj(x;T) cannotbe proven, because it's antecedent would involve the subtypepredicate which isn't typeable. |
| def | type_inj |
[x]{T} == x |
| THM | fun_thru_spread |
 B:(A B:(A  Type), p:(x:A Type), p:(x:A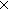 B(x)), C,D:Type, f:(C B(x)), C,D:Type, f:(C  D), b:(x:A D), b:(x:A  B(x) B(x)  C). C).
f(p/x,y. b(x,y)) = (p/x,y. f(b(x,y))) |
| THM | spread_to_pi12 |
 B:(A B:(A  Type), p:(x:A Type), p:(x:A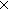 B(x)), C:Type, b:(x:A B(x)), C:Type, b:(x:A  B(x) B(x)  C). C).
(p/x,y. b(x,y)) = b(1of(p),2of(p)) |
| def | singleton |
{a:T} == {x:T| x = a 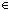 T } T } |
| THM | singleton_properties |
 a:T, x:{a:T}. x = a a:T, x:{a:T}. x = a 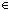 T T |
| def | unique_set |
{!x:T | P(x)} == {x:T| P(x) & ( y:T. P(y) y:T. P(y)   y = x) } y = x) } |
| def | uni_sat |
a = !x:T. Q(x) == Q(a) & ( a':T. Q(a') a':T. Q(a')   a' = a) a' = a) |
| THM | uni_sat_imp_in_uni_set |
 a:T, Q:(T a:T, Q:(T  Prop). (a = !x:T. Q(x)) Prop). (a = !x:T. Q(x))   a a 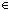 {!x:T | Q(x)} {!x:T | Q(x)} |
| def | ycomb |
Y(f) == (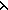 x.f(x(x)))( x.f(x(x)))(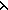 x.f(x(x))) x.f(x(x))) |