Selected Objects
| def | discrete | Discrete{T} ==  x,y:T. Dec(x = y) x,y:T. Dec(x = y) |
| THM | discrete_implies_bool_equality | Discrete{T} 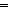 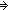 ( (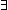 f:(T f:(T 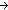 T T 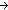 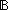 ). ).  x,y:T. f(x,y) x,y:T. f(x,y) 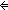 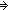 x = y) x = y) |
| def | discrete_equality | {T=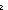 } == {eq:(T } == {eq:(T 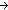 T T 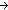 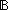 )| )|  x,y:T. eq(x,y) x,y:T. eq(x,y) 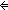 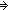 x = y } x = y } |
| THM | discrete_equality_inc | {T=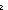 } } 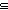 (T (T 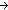 T T 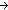 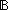 ) ) |
| THM | discrete_equality_properties |  eq:{T= eq:{T=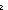 }. ( }. ( x,y:T. eq(x,y) x,y:T. eq(x,y) 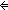 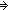 x = y) & eq x = y) & eq 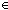 T T 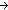 T T 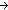 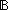 |
| THM | discrete_implies_discrete_equality | Discrete{T} 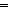 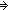 ( (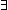 f:{T= f:{T=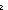 }. True) }. True) |
| THM | discrete_equality_unique |  f1,f2:{T= f1,f2:{T=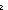 }. f1 = f2 }. f1 = f2 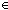 T T 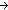 T T 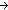  |
| THM | discrete_equality_reflexive |  eq:{T= eq:{T=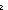 }, u:T. eq(u,u) }, u:T. eq(u,u) |
| THM | discrete_equality_symmetric |  eq:{T= eq:{T=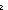 }, x,y:T. eq(x,y) }, x,y:T. eq(x,y) 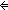 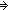 eq(y,x) eq(y,x) |
| THM | discrete_equality_transitive |  eq:{T= eq:{T=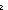 }, x,y,z:T. eq(x,y) }, x,y,z:T. eq(x,y) 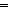 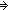 eq(y,z) eq(y,z) 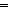 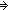 eq(x,z) eq(x,z) |
| THM | discrete__union |  T1:Type{i}, T2:Type{j}. Discrete{T1} T1:Type{i}, T2:Type{j}. Discrete{T1} 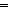 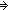 Discrete{T2} Discrete{T2} 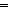 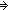 Discrete{(T1+T2)} Discrete{(T1+T2)} |
| THM | discrete__product |  T1:Type{i}, T2:Type{j}. Discrete{T1} T1:Type{i}, T2:Type{j}. Discrete{T1} 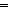 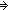 Discrete{T2} Discrete{T2} 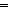 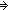 Discrete{(T1 Discrete{(T1 T2)} T2)} |
| THM | discrete__atom | Discrete{Atom} |