Selected Objects
| THM | nat_add |  n,m: n,m: . n+m . n+m   |
| THM | nat_mul |  n,m: n,m: . n . n m m   |
| THM | zero_length_imp_nil |  l:T*. ||l|| = 0 l:T*. ||l|| = 0   l = nil l = nil |
| THM | rem_quo_unique |  n: n: 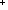 , r1,r2: , r1,r2: n, q1,q2: n, q1,q2: . r1+q1 . r1+q1 n = r2+q2 n = r2+q2 n n   r1 = r2 & q1 = q2 r1 = r2 & q1 = q2 |
| THM | div_lt_lbound |  a: a: , n: , n: 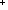 , k: , k: . a < n . a < n k k   (a (a 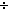 n) < k n) < k |
| def | en | (rec) en(l) == if null(l)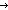 0 else hd(l)+en(tl(l)) 0 else hd(l)+en(tl(l)) n fi n fi |
| THM | en_inj |  n: n: 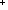 , m: , m: , l1,l2: , l1,l2: n*. ||l1|| = m & ||l2|| = m n*. ||l1|| = m & ||l2|| = m   en(l1) = en(l2) en(l1) = en(l2)   l1 = l2 l1 = l2 |
| def | exp | (rec) (base power) == if power= power) == if power=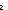 0 0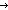 1 else base 1 else base (base (base power-1) fi power-1) fi |
| THM | exp_functionality |  n1,n2,k1,k2: n1,n2,k1,k2: . n1 = n2 . n1 = n2   k1 = k2 k1 = k2   (n1 (n1 k1) = (n2 k1) = (n2 k2) k2) |
| THM | exp_zero |  m: m: 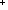 . (0 . (0 m) = 0 m) = 0 |
| THM | exp_non_zero |  m: m: 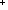 , n: , n: . 0 < (m . 0 < (m n) n) |
| THM | exp_base |  n: n: . (n . (n 0) = 1 0) = 1 |
| THM | exp_step |  n,k: n,k: . 0 < k . 0 < k   (n (n k) = n k) = n (n (n k-1) k-1) |
| THM | fun_enumer |  n,m: n,m: . .  f:(( f:(( m m   n) n)   (n (n m)). Bij( m)). Bij( m m   n; n;  (n (n m); f) m); f) |
| THM | auto2_lemma_0 |  P:(T P:(T  Prop). ( Prop). ( x:T. Dec(P(x))) & Dec( x:T. Dec(P(x))) & Dec( x:T. x:T. 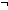 P(x)) P(x))   Dec( Dec( x:T. P(x)) x:T. P(x)) |
| THM | auto2_lemma_1 |  P,Q:(T P,Q:(T  Prop). ( Prop). ( t:T. P(t) t:T. P(t) 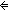  Q(t)) Q(t))   ({t:T| P(t) } ~ {t:T| Q(t) }) ({t:T| P(t) } ~ {t:T| Q(t) }) |
| THM | auto2_lemma_3 |  R:(Alph* R:(Alph*  Alph* Alph*  Prop), n: Prop), n: 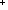 .
( .
( x:Alph*. R(x,x))
& ( x:Alph*. R(x,x))
& ( x,y:Alph*. R(x,y) x,y:Alph*. R(x,y)   R(y,x))
& ( R(y,x))
& ( x,y,z:Alph*. R(x,y) & R(y,z) x,y,z:Alph*. R(x,y) & R(y,z)   R(x,z))
& ( R(x,z))
& ( x,y,z:Alph*. R(x,y) x,y,z:Alph*. R(x,y)   R((z @ x),z @ y))
& ( R((z @ x),z @ y))
& ( w:( w:( n n  Alph*). Alph*).  l:Alph*. l:Alph*.  i: i: n. R(l,w(i))) n. R(l,w(i)))
  (
( a,b,c:Alph*. ||a|| a,b,c:Alph*. ||a||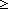 n n n n   ( ( a':Alph*. ||a'|| < ||a|| & R((a @ b),a' @ b) & R((a @ c),a' @ c))) a':Alph*. ||a'|| < ||a|| & R((a @ b),a' @ b) & R((a @ c),a' @ c))) |
| THM | auto2_lemma_4 |  R:(Alph* R:(Alph*  Alph* Alph*  Prop), n: Prop), n: 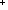 .
( .
( x:Alph*. R(x,x))
& ( x:Alph*. R(x,x))
& ( x,y:Alph*. R(x,y) x,y:Alph*. R(x,y)   R(y,x))
& ( R(y,x))
& ( x,y,z:Alph*. R(x,y) & R(y,z) x,y,z:Alph*. R(x,y) & R(y,z)   R(x,z))
& ( R(x,z))
& ( x,y,z:Alph*. R(x,y) x,y,z:Alph*. R(x,y)   R((z @ x),z @ y))
& ( R((z @ x),z @ y))
& ( w:( w:( n n  Alph*). Alph*).  l:Alph*. l:Alph*.  i: i: n. R(l,w(i))) n. R(l,w(i)))
  (
( a,b,c:Alph*. a,b,c:Alph*.  a':Alph*. ||a'|| < n a':Alph*. ||a'|| < n n & R((a @ b),a' @ b) & R((a @ c),a' @ c)) n & R((a @ b),a' @ b) & R((a @ c),a' @ c)) |
| THM | auto2_lemma_5 |  n: n: . Fin(Alph) . Fin(Alph)   Fin({l:(Alph*)| ||l|| = n }) Fin({l:(Alph*)| ||l|| = n }) |
| THM | auto2_lemma_6 |  R:(T R:(T  Prop). Fin(T) & ( Prop). Fin(T) & ( t:T. Dec(R(t))) t:T. Dec(R(t)))   Dec( Dec( t:T. R(t)) t:T. R(t)) |
| THM | auto2_lemma_7 |  R:(Alph* R:(Alph*  Alph* Alph*  Prop), n: Prop), n: 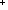 , L:(Alph* , L:(Alph*  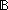 ), m: ), m: .
( .
( x:Alph*. R(x,x))
& ( x:Alph*. R(x,x))
& ( x,y:Alph*. R(x,y) x,y:Alph*. R(x,y)   R(y,x))
& ( R(y,x))
& ( x,y,z:Alph*. R(x,y) & R(y,z) x,y,z:Alph*. R(x,y) & R(y,z)   R(x,z))
& ( R(x,z))
& ( x,y,z:Alph*. R(x,y) x,y,z:Alph*. R(x,y)   R((z @ x),z @ y))
& ( R((z @ x),z @ y))
& ( w:( w:( n n  Alph*). Alph*).  l:Alph*. l:Alph*.  i: i: n. R(l,w(i)))
& ( n. R(l,w(i)))
& ( v:( v:( m m  Alph*). Alph*).  l:Alph*. L(l) l:Alph*. L(l) 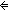  ( ( i: i: m. R(l,v(i))))
& Fin(Alph) m. R(l,v(i))))
& Fin(Alph)
  (
( x,y:Alph*. Dec( x,y:Alph*. Dec( l:Alph*. l:Alph*. 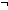 L(l @ x) = L(l @ y))) L(l @ x) = L(l @ y))) |
| THM | auto2_lemma_8 |  R:(Alph* R:(Alph*  Alph* Alph*  Prop), n: Prop), n: 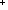 , L:(Alph* , L:(Alph*  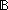 ), m: ), m: .
( .
( x:Alph*. R(x,x))
& ( x:Alph*. R(x,x))
& ( x,y:Alph*. R(x,y) x,y:Alph*. R(x,y)   R(y,x))
& ( R(y,x))
& ( x,y,z:Alph*. R(x,y) & R(y,z) x,y,z:Alph*. R(x,y) & R(y,z)   R(x,z))
& ( R(x,z))
& ( x,y,z:Alph*. R(x,y) x,y,z:Alph*. R(x,y)   R((z @ x),z @ y))
& ( R((z @ x),z @ y))
& ( w:( w:( n n  Alph*). Alph*).  l:Alph*. l:Alph*.  i: i: n. R(l,w(i)))
& ( n. R(l,w(i)))
& ( v:( v:( m m  Alph*). Alph*).  l:Alph*. L(l) l:Alph*. L(l) 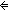  ( ( i: i: m. R(l,v(i))))
& Fin(Alph) m. R(l,v(i))))
& Fin(Alph)
  (
( x,y:Alph*. Dec( x,y:Alph*. Dec( l:Alph*. L(l @ x) = L(l @ y))) l:Alph*. L(l @ x) = L(l @ y))) |
| THM | fun_preserves_fin | Fin(S) & Fin(T)   Fin(S Fin(S  T) T) |
| THM | en_ubound |  n: n: , l: , l: n*. en(l) < (n n*. en(l) < (n ||l||) ||l||) |
| THM | en_bound |  n: n: , l: , l: n*. en(l) n*. en(l)   (n (n ||l||) ||l||) |
| THM | en_surj |  n: n: 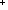 , m: , m: , k: , k: (n (n m). m).  l: l: n*. ||l|| = m & en(l) = k n*. ||l|| = m & en(l) = k |
| def | geom_series | (rec) 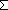 (q (q n n ) == if n= ) == if n=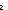 0 0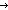 0 else 0 else 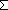 (q (q n-1 n-1 )+(q )+(q n-1) fi n-1) fi |
| THM | geom_series_step |  q,n: q,n: . . 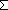 (q (q n+1 n+1 ) = ) = 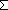 (q (q n n )+(q )+(q n) n)   |
| THM | geom_ndecrease |  q,n,i: q,n,i: . . 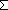 (q (q n n ) )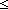 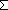 (q (q n+i n+i ) ) |
| THM | geom_speed_lbound |  q,n: q,n: , i: , i: 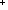 . . 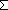 (q (q n n )+(q )+(q n) n)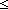 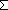 (q (q n+i n+i ) ) |
| THM | geom_n_unique |  q: q: 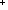 , n: , n: , i: , i: 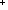 , r1: , r1: (q (q n), r2: n), r2: (q (q n+i). n+i). 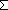 (q (q n n )+r1 = )+r1 = 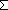 (q (q n+i n+i )+r2 )+r2   False False |
| THM | geom_unique |  q: q: 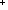 , n1,n2: , n1,n2: , r1: , r1: (q (q n1), r2: n1), r2: (q (q n2). n2). 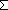 (q (q n1 n1 )+r1 = )+r1 = 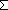 (q (q n2 n2 )+r2 )+r2   n1 = n2 & r1 = r2 n1 = n2 & r1 = r2   |
| THM | geom_series_limit |  q: q: 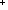 , a: , a: . .  n: n: . . 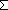 (q (q n n ) ) 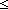 a < a < 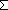 (q (q n+1 n+1 ) ) |
| def | enum | enum(l) == 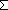 (q (q ||l|| ||l|| )+en(l) )+en(l) |
| THM | enum_inj |  q: q: 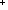 , l1,l2: , l1,l2: q*. enum(l1) = enum(l2) q*. enum(l1) = enum(l2)   l1 = l2 l1 = l2 |
| THM | enum_surj |  q: q: 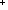 , a: , a: . .  l: l: q*. enum(l) = a q*. enum(l) = a |
| THM | list_1_1_nat |  q: q: 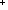 . ( . ( q*) ~ q*) ~  |