| 1 | 1. Alph: Type
2. R: Alph*  Alph* Alph*  Prop Prop
3. n:  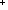
4. ( x:Alph*. R(x,x))
& ( x:Alph*. R(x,x))
& ( x,y:Alph*. R(x,y) x,y:Alph*. R(x,y)   R(y,x))
& ( R(y,x))
& ( x,y,z:Alph*. R(x,y) & R(y,z) x,y,z:Alph*. R(x,y) & R(y,z)   R(x,z))
& ( R(x,z))
& ( x,y,z:Alph*. R(x,y) x,y,z:Alph*. R(x,y)   R((z @ x),z @ y))
& ( R((z @ x),z @ y))
& ( w:( w:( n n  Alph*). Alph*).  l:Alph*. l:Alph*.  i: i: n. R(l,w(i))) n. R(l,w(i)))
5. a: Alph*
6. b: Alph*
7. c: Alph*
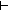  a':Alph*. ||a'|| < n a':Alph*. ||a'|| < n n & R((a @ b),a' @ b) & R((a @ c),a' @ c) n & R((a @ b),a' @ b) & R((a @ c),a' @ c) |