Selected Objects
| THM | not_dec_is_dec |  P:(A P:(A  Prop). ( Prop). ( x:A. P(x) x:A. P(x) 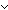 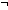 P(x)) & ( P(x)) & ( x:A. x:A. 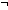 P(x)) P(x)) 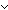 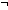 ( ( x:A. x:A. 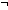 P(x)) P(x))   ( ( x:A. P(x)) x:A. P(x)) 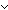 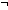 ( ( x:A. P(x)) x:A. P(x)) |
| THM | rect_enumer |  n,m: n,m: 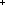 . .  f:( f:( n n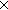  m m   (n (n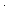 m)). Bij( m)). Bij( n n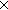  m; m;  (n (n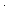 m); f) m); f) |
| def | finite | Fin(s) ==  n: n: , f:( , f:( n n  s). Bij( s). Bij( n; s; f) n; s; f) |
| THM | nsub_is_finite |  n: n: . Fin( . Fin( n) n) |
| THM | bool_is_finite | Fin(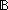 ) ) |
| THM | one2one_preserves_fin | (T ~ U) & Fin(T)   Fin(U) Fin(U) |
| THM | fin_iff_1_1_nsub | Fin(T) 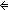  ( ( m: m: . .  m ~ T) m ~ T) |
| THM | div_bounds_2 |  n: n: 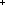 , x: , x: (n (n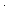 n). (x n). (x 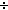 n) < n n) < n |
| THM | prod_fin_is_fin |  t:T. Fin(T) t:T. Fin(T)   Fin(T Fin(T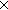 T) T) |
| THM | fin_dec_fin |  n: n: , T:Type, B:(T , T:Type, B:(T  Prop). ( Prop). ( n ~ T) & ( n ~ T) & ( t:T. Dec(B(t))) t:T. Dec(B(t)))   ( ( m: m: . .  m ~ {t:T| B(t) }) m ~ {t:T| B(t) }) |
| THM | finite_decidable_subset |  B:(T B:(T  Prop). Fin(T) & ( Prop). Fin(T) & ( t:T. Dec(B(t))) t:T. Dec(B(t)))   Fin({t:T| B(t) }) Fin({t:T| B(t) }) |
| THM | one_one_preser_fin | Fin(T) & (T ~ S)   Fin(S) Fin(S) |
| THM | set_function |  R:(S R:(S  T T  Prop).
( Prop).
( s:S. Dec( s:S. Dec( t:T. R(s,t))) t:T. R(s,t)))   ( ( f:({s:S| f:({s:S|  t:T. R(s,t) } t:T. R(s,t) }  T). T).  s:{s:S| s:{s:S|  t:T. R(s,t) }. R(s,f(s))) t:T. R(s,t) }. R(s,f(s))) |
| THM | inv_of_fin_is_fin |  f:(T f:(T  S). Fin(S) & ( S). Fin(S) & ( s:S. Dec( s:S. Dec( t:T. f(t) = s)) t:T. f(t) = s))   Fin(x,y:T//(f(x) = f(y))) Fin(x,y:T//(f(x) = f(y))) |
| THM | fin_is_decid | Fin(T)   ( ( x,y:T. Dec(x = y)) x,y:T. Dec(x = y)) |
| THM | fin_dist_func | Fin(St)   ( ( eq:(St eq:(St  St St  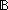 ). ).  x,y:St. eq(x,y) x,y:St. eq(x,y)   x = y) x = y) |
| THM | decid_is_comp |  f:(T f:(T  Prop). ( Prop). ( t:T. Dec(f(t))) t:T. Dec(f(t)))   ( ( g:(T g:(T  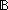 ). ).  t:T. f(t) t:T. f(t) 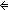  g(t)) g(t)) |
| THM | auto2_list_ind |  P:(Alph* P:(Alph*  Prop).
( Prop).
( n: n: . ( . ( l:Alph*. ||l|| < n l:Alph*. ||l|| < n   P(l)) P(l))   ( ( l:Alph*. ||l|| = n l:Alph*. ||l|| = n   P(l))) P(l)))   ( ( l:Alph*. P(l)) l:Alph*. P(l)) |
| THM | one_one_sym | (T ~ S)   (S ~ T) (S ~ T) |
| COM | phole_descr | Pigeon-hole principle |
| THM | phole_aux |  n:{1...}, f:( n:{1...}, f:( (n+1) (n+1)   n). n).  i: i: (n+1), j: (n+1), j: i. f(i) = f(j) i. f(i) = f(j) |
| THM | phole_lemma |  n:{1...}, m:{n+1...}, f:( n:{1...}, m:{n+1...}, f:( m m   n). n).  i,j: i,j: m. i < j & f(i) = f(j) m. i < j & f(i) = f(j) |
| def | card | #(t)=n == t ~  n n |