| Rank | Theorem | Name |
| 8 | Thm*  x,y: x,y: , n: , n:  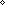 . ((x+y) rem n) = (((x rem n)+(y rem n)) rem n)+if (x+y < . ((x+y) rem n) = (((x rem n)+(y rem n)) rem n)+if (x+y < 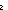 0) 0)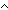 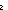 (0 < (0 < 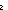 (((x rem n)+(y rem n)) rem n)) (((x rem n)+(y rem n)) rem n)) -|n| ;((((x rem n)+(y rem n)) rem n) < -|n| ;((((x rem n)+(y rem n)) rem n) < 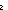 0) 0)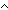 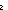 (0 < (0 < 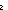 x+y) x+y) |n| else 0 fi |n| else 0 fi | [rem_add] |
| cites |
| 1 | Thm*  a: a: , n: , n:  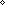 . a = (a . a = (a 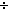 n) n) n+(a rem n) & |a rem n| < |n| & ((a rem n) < 0 n+(a rem n) & |a rem n| < |n| & ((a rem n) < 0   a < 0) & ((a rem n) > 0 a < 0) & ((a rem n) > 0   a > 0) a > 0) | [div_rem_properties] |
| 7 | Thm*  x: x: , n: , n:  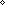 . ((-x) rem n) = -(x rem n) . ((-x) rem n) = -(x rem n) | [rem_minus] |
| 7 | Thm*  n: n:  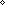 . (0 rem n) = 0 . (0 rem n) = 0 | [zero_rem] |
| 6 | Thm*  a: a: , n: , n:  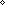 , q,r: , q,r: . a = q . a = q n+r n+r   |r| < |n| |r| < |n|   (r < 0 (r < 0   a < 0) a < 0)   (r > 0 (r > 0   a > 0) a > 0)   q = (a q = (a 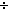 n) & r = (a rem n) n) & r = (a rem n) | [div_rem_unique] |