At:
mapoutl is append
1
2
2
1
1.
A: Type
2.
B: Type
3.
l1: A List
4.
l2: A List
5.
u: A
6.
v: A List
7.
L:(A+B) List.
mapoutl(L) = (v @ l2) 
(
L1,L2:(A+B) List. L = (L1 @ L2) & mapoutl(L1) = v & mapoutl(L2) = l2)
8.
L: (A+B) List
9.
x: A
10.
v1: (A+B) List
11.
mapoutl(v1) = [u / (v @ l2)]
(L1,L2:(A+B) List. v1 = (L1 @ L2) & mapoutl(L1) = [u / v] & mapoutl(L2) = l2)
12.
[x / mapoutl(v1)] = [u / (v @ l2)]
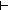
L1,L2:(A+B) List. [inl(x) / v1] = (L1 @ L2) & mapoutl(L1) = [u / v] & mapoutl(L2) = l2
By:
SplitCons -1
THEN
InstHyp [v1] 7
THEN
ExRepD
THEN
InstConcl [[inl(x) / L1];L2]
THEN
Reduce 0
THEN
Analyze
Generated subgoals:
None
About:
