| Rank | Theorem | Name |
| 6 | Thm*  k: k:  , L: , L: List. 0 < ||L|| List. 0 < ||L||   ( ( r: r:  . r- > L^k) . r- > L^k) | [Ramsey] |
| cites |
| 4 | Thm*  L: L: List. sum(L[i]-1 | i < ||L||)+1- > L^1 List. sum(L[i]-1 | i < ||L||)+1- > L^1 | [Ramsey-base-case] |
| 0 | Thm*  k: k:  , L: , L: List, r1,r2: List, r1,r2: . r1 . r1 r2 r2   r1- > L^k r1- > L^k   r2- > L^k r2- > L^k | [arrows-monotone1] |
| 5 | Thm*  k: k:  , L: , L: List. k-1- > L^k List. k-1- > L^k   ( ( i: i: ||L||. L[i] < k) ||L||. L[i] < k) | [trivial-arrows] |
| 0 | Thm*  k,b: k,b: , f:( , f:( k k   ). ( ). ( x: x: k. b k. b f(x)) f(x))   b b k k sum(f(x) | x < k) sum(f(x) | x < k) | [sum_lower_bound] |
| 1 | Thm*  n: n: , f,g:( , f,g:( n n   ), d: ), d: . sum(f(x)-g(x) | x < n) = d . sum(f(x)-g(x) | x < n) = d   sum(f(x) | x < n) = sum(g(x) | x < n)+d sum(f(x) | x < n) = sum(g(x) | x < n)+d | [sum_difference] |
| 2 | Thm*  n: n: , f:( , f:( n n   ), m: ), m: n. ( n. ( x: x: n. n.  x = m x = m   f(x) = 0) f(x) = 0)   sum(f(x) | x < n) = f(m) sum(f(x) | x < n) = f(m) | [singleton_support_sum] |
| 3 | Thm*  L: L: List, i,j: List, i,j: ||L||. 0 < L[i] ||L||. 0 < L[i]   L[i--][j] = if j= L[i--][j] = if j=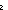 i i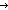 L[j]-1 else L[j] fi L[j]-1 else L[j] fi | [list-dec-select] |
| 0 | Thm*  n: n: , f:( , f:( n n   ). ( ). ( x: x: n. 0 n. 0 f(x)) f(x))   0 0 sum(f(x) | x < n) sum(f(x) | x < n) | [non_neg_sum] |
| 2 | Thm*  L: L: List, i: List, i: ||L||. 0 < L[i] ||L||. 0 < L[i]   ||L[i--]|| = ||L|| ||L[i--]|| = ||L||   | [list-dec-length] |
| 2 | Thm*  n: n: , f:( , f:( n n  T), i: T), i: n. mklist(n;f)[i] = f(i) n. mklist(n;f)[i] = f(i) | [mklist_select] |
| 1 | Thm*  n: n: , f:( , f:( n n  T). ||mklist(n;f)|| = n T). ||mklist(n;f)|| = n   | [mklist_length] |
| 4 | Thm*  r,k: r,k: , L,R: , L,R: List. 2 List. 2 k k   ||R|| = ||L|| ||R|| = ||L||     ( ( i: i: ||L||. 0 < L[i] ||L||. 0 < L[i]   R[i]- > L[i--]^k) R[i]- > L[i--]^k)   r- > R^k-1 r- > R^k-1   r+1- > L^k r+1- > L^k | [Ramsey-recursion] |