Selected Objects
| def | mod_guard | mod_guard(x;y) == x mod y |
| THM | mod_add_guard |  x,y: x,y: , n: , n:  . ((x+y) mod n) = mod_guard((x mod n)+(y mod n);n) . ((x+y) mod n) = mod_guard((x mod n)+(y mod n);n) |
| THM | mod_mul_guard |  x,y: x,y: , n: , n:  . ((x . ((x y) mod n) = mod_guard((x mod n) y) mod n) = mod_guard((x mod n) (y mod n);n) (y mod n);n) |
| THM | elim_divides |  x: x: , n: , n:  . (n | x) . (n | x)   (x mod n) = 0 (x mod n) = 0 |
| THM | sqrt_prime_irrational |  p: p:  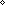 . prime(p) . prime(p)   ( ( m,n: m,n: . m . m m = p m = p n n n n   n = 0) n = 0) |
| THM | fappend-increasing |  n,m: n,m:  , f:( , f:( (n-1) (n-1)   (m-1)). increasing(f;n-1) (m-1)). increasing(f;n-1)   increasing(f[n-1:=m-1];n) increasing(f[n-1:=m-1];n) |
| THM | fappend-inject |  n,m: n,m:  , f:( , f:( (n-1) (n-1)   (m-1)). Inj( (m-1)). Inj( (n-1); (n-1);  (m-1); f) (m-1); f)   Inj( Inj( n; n;  m; f[n-1:=m-1]) m; f[n-1:=m-1]) |
| THM | finite-partition |  n,k: n,k: , c:( , c:( n n   k). k).  p:( p:( k k  ( ( List)). sum(||p(j)|| | j < k) = n & ( List)). sum(||p(j)|| | j < k) = n & ( j: j: k, x,y: k, x,y: ||p(j)||. x < y ||p(j)||. x < y   (p(j))[x] > (p(j))[y]) & ( (p(j))[x] > (p(j))[y]) & ( j: j: k, x: k, x: ||p(j)||. (p(j))[x] < n & c((p(j))[x]) = j) ||p(j)||. (p(j))[x] < n & c((p(j))[x]) = j) |
| THM | pigeon-hole |  n,m: n,m: , f:( , f:( n n   m). Inj( m). Inj( n; n;  m; f) m; f)   n n m m |
| def | arrows | r- > L^k ==  n: n: . r . r n n   ( ( G:({s:( G:({s:( n List)| ||s|| = k n List)| ||s|| = k   & ( & ( x,y: x,y: ||s||. x < y ||s||. x < y   s[x] < s[y]) } s[x] < s[y]) }   ||L||). ||L||).  c: c: ||L||, f:( ||L||, f:( L[c] L[c]   n). increasing(f;L[c]) & ( n). increasing(f;L[c]) & ( s: s: L[c] List. ||s|| = k L[c] List. ||s|| = k     ( ( x,y: x,y: ||s||. x < y ||s||. x < y   s[x] < s[y]) s[x] < s[y])   G(map(f;s)) = c)) G(map(f;s)) = c)) |
| THM | trivial-arrows |  k: k:  , L: , L: List. k-1- > L^k List. k-1- > L^k   ( ( i: i: ||L||. L[i] < k) ||L||. L[i] < k) |
| THM | arrows-monotone1 |  k: k:  , L: , L: List, r1,r2: List, r1,r2: . r1 . r1 r2 r2   r1- > L^k r1- > L^k   r2- > L^k r2- > L^k |
| THM | Ramsey-base-case |  L: L: List. sum(L[i]-1 | i < ||L||)+1- > L^1 List. sum(L[i]-1 | i < ||L||)+1- > L^1 |
| def | list-dec | L[i--] == mklist(||L||;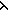 j.if j= j.if j=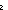 i i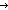 L[j]-1 else L[j] fi) L[j]-1 else L[j] fi) |
| THM | list-dec-length |  L: L: List, i: List, i: ||L||. 0 < L[i] ||L||. 0 < L[i]   ||L[i--]|| = ||L|| ||L[i--]|| = ||L||   |
| THM | list-dec-select |  L: L: List, i,j: List, i,j: ||L||. 0 < L[i] ||L||. 0 < L[i]   L[i--][j] = if j= L[i--][j] = if j=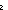 i i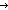 L[j]-1 else L[j] fi L[j]-1 else L[j] fi |
| THM | Ramsey-recursion |  r,k: r,k: , L,R: , L,R: List. 2 List. 2 k k   ||R|| = ||L|| ||R|| = ||L||     ( ( i: i: ||L||. 0 < L[i] ||L||. 0 < L[i]   R[i]- > L[i--]^k) R[i]- > L[i--]^k)   r- > R^k-1 r- > R^k-1   r+1- > L^k r+1- > L^k |
| THM | Ramsey |  k: k:  , L: , L: List. 0 < ||L|| List. 0 < ||L||   ( ( r: r:  . r- > L^k) . r- > L^k) |
| def | paren | (rec) paren(T;s) == s = nil  (T+T) List (T+T) List 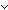 ( ( t:T, s':(T+T) List. s = ([inl(t)] @ s' @ [inr(t)]) & paren(T;s')) t:T, s':(T+T) List. s = ([inl(t)] @ s' @ [inr(t)]) & paren(T;s')) 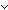 ( ( s',s'':(T+T) List. ||s'|| < ||s|| & ||s''|| < ||s|| & s = (s' @ s'') & paren(T;s') & paren(T;s'')) s',s'':(T+T) List. ||s'|| < ||s|| & ||s''|| < ||s|| & s = (s' @ s'') & paren(T;s') & paren(T;s'')) |
| THM | paren_induction |  P:(((T+T) List) P:(((T+T) List)  Prop). P(nil) Prop). P(nil)   ( ( s1,s2:(T+T) List. P(s1) s1,s2:(T+T) List. P(s1)   P(s2) P(s2)   paren(T;s1) paren(T;s1)   paren(T;s2) paren(T;s2)   P(s1 @ s2)) P(s1 @ s2))   ( ( s:(T+T) List, t:T. P(s) s:(T+T) List, t:T. P(s)   paren(T;s) paren(T;s)   P([inl(t)] @ s @ [inr(t)])) P([inl(t)] @ s @ [inr(t)]))   ( ( s:(T+T) List. paren(T;s) s:(T+T) List. paren(T;s)   P(s)) P(s)) |
| THM | paren_balance1 |  s':(T+T) List. paren(T;s') s':(T+T) List. paren(T;s')   ( ( i:T. (inl(i) i:T. (inl(i)  s') s')   (inr(i) (inr(i)  s')) s')) |
| def | member-paren | member-paren(x,y.E(x;y);i;s) == ( x x s.InjCase(x; a. E(a;i), E(a;i))) s.InjCase(x; a. E(a;i), E(a;i))) |
| THM | assert-member-paren |  E:(T E:(T  T T  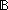 ). ( ). ( x,y:T. E(x,y) x,y:T. E(x,y)   x = y) x = y)   ( ( i:T, s:(T+T) List. member-paren(x,y.E(x,y);i;s) i:T, s:(T+T) List. member-paren(x,y.E(x,y);i;s)   (inl(i) (inl(i)  s) s) 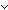 (inr(i) (inr(i)  s)) s)) |
| def | member-right-paren | member-right-paren(x,y.E(x;y);i;s) == ( x x s.InjCase(x; a. false s.InjCase(x; a. false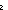 , E(a;i))) , E(a;i))) |
| THM | assert-member-right-paren |  E:(T E:(T  T T  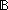 ). ( ). ( x,y:T. E(x,y) x,y:T. E(x,y)   x = y) x = y)   ( ( i:T, s:(T+T) List. member-right-paren(x,y.E(x,y);i;s) i:T, s:(T+T) List. member-right-paren(x,y.E(x,y);i;s)   (inr(i) (inr(i)  s)) s)) |
| def | member-left-paren | member-left-paren(x,y.E(x;y);i;s) == ( x x s.InjCase(x; a. E(a;i), false s.InjCase(x; a. E(a;i), false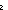 )) )) |
| THM | assert-member-left-paren |  E:(T E:(T  T T  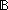 ). ( ). ( x,y:T. E(x,y) x,y:T. E(x,y)   x = y) x = y)   ( ( i:T, s:(T+T) List. member-left-paren(x,y.E(x,y);i;s) i:T, s:(T+T) List. member-left-paren(x,y.E(x,y);i;s)   (inl(i) (inl(i)  s)) s)) |
| THM | paren_balance2 |  s':(T+T) List. paren(T;s') s':(T+T) List. paren(T;s')   ( ( i:T. (inr(i) i:T. (inr(i)  s') s')   (inl(i) (inl(i)  s')) s')) |
| THM | append_paren |  s',s3:(T+T) List. paren(T;s') s',s3:(T+T) List. paren(T;s')   paren(T;s3) paren(T;s3)   paren(T;s3 @ s') paren(T;s3 @ s') |
| THM | paren_order1 |  s:(T+T) List. paren(T;s) s:(T+T) List. paren(T;s)   ( ( i:T, s1,s2:(T+T) List. s = (s1 @ [inl(i)] @ s2) i:T, s1,s2:(T+T) List. s = (s1 @ [inl(i)] @ s2)   (inr(i) (inr(i)  s2)) s2)) |
| THM | paren_interval |  s:(T+T) List. paren(T;s) s:(T+T) List. paren(T;s)   no_repeats(T+T;s) no_repeats(T+T;s)   ( ( s1,s2,s3:(T+T) List, x:T. s = (s1 @ [inl(x)] @ s2 @ [inr(x)] @ s3) s1,s2,s3:(T+T) List, x:T. s = (s1 @ [inl(x)] @ s2 @ [inr(x)] @ s3)   paren(T;s2)) paren(T;s2)) |
| THM | decidable__l_member_paren | ( x,y:T. Dec(x = y)) x,y:T. Dec(x = y))   ( ( s:(T+T) List, i:T. Dec((inl(i) s:(T+T) List, i:T. Dec((inl(i)  s))) s))) |
| def | array | array(T) == n:   n n  T T |
| def | array-length | |a| == 1of(a) |
| def | array-select | a[i] == 2of(a)(i) |
| def | array-update | a[i:=v] == < |a|,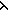 j.if j= j.if j=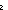 i i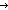 v else a[j] fi > v else a[j] fi > |
| THM | array-update-select |  a:array(T), j,i: a:array(T), j,i: |a|, v:T. a[i:=v][j] ~ if j= |a|, v:T. a[i:=v][j] ~ if j=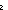 i i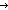 v else a[j] fi v else a[j] fi |
| def | array-const | array[n]:=v == < n,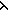 i.v > i.v > |
| def | array-count | array-count(v.P(v);a) == sum(if P(a[i])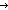 1 else 0 fi | i < |a|) 1 else 0 fi | i < |a|) |
| THM | array-count-update |  P:(T P:(T  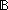 ), a:array(T), i: ), a:array(T), i: |a|, v:T. array-count(v.P(v);a[i:=v]) = array-count(v.P(v);a)+if P(v) |a|, v:T. array-count(v.P(v);a[i:=v]) = array-count(v.P(v);a)+if P(v)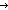 if P(a[i]) if P(a[i])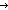 0 else 1 fi ;P(a[i]) 0 else 1 fi ;P(a[i])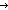 -1 else 0 fi -1 else 0 fi |
| def | graph | Graph == v:Type e:Type e:Type (e (e  v v v) v) Top Top |
| def | gr_v | Vertices(t) == 1of(t) |
| def | gr_e | Edges(t) == 1of(2of(t)) |
| def | gr_f | Incidence(t) == 1of(2of(2of(t))) |
| def | gr_o | t.o == 2of(2of(2of(t))) |
| def | mkgraph | < vertices = v, edges = e, incidence = f > == < v,e,f,o > |
| def | edge | x-the_graph- > y ==  e:Edges(the_graph). Incidence(the_graph)(e) = < x,y > e:Edges(the_graph). Incidence(the_graph)(e) = < x,y > |
| def | path | path(the_graph;p) == 0 < ||p|| & ( i: i: (||p||-1). p[i]-the_graph- > p[(i+1)]) (||p||-1). p[i]-the_graph- > p[(i+1)]) |
| def | connect | x-the_graph- > *y ==  p:Vertices(the_graph) List. path(the_graph;p) & p[0] = x & last(p) = y p:Vertices(the_graph) List. path(the_graph;p) & p[0] = x & last(p) = y |
| THM | connect_transitivity | For any graph
 x,y,z:V. x-the_graph- > *y x,y,z:V. x-the_graph- > *y   y-the_graph- > *z y-the_graph- > *z   x-the_graph- > *z x-the_graph- > *z |
| THM | connect_weakening | For any graph
 x,y:V. x = y x,y:V. x = y   x-the_graph- > *y x-the_graph- > *y |
| THM | edge-connect | For any graph
 x,y:V. x-the_graph- > y x,y:V. x-the_graph- > y   x-the_graph- > *y x-the_graph- > *y |
| THM | path-tl | For any graph
 p:V List. 1 < ||p|| p:V List. 1 < ||p||   path(the_graph;p) path(the_graph;p)   path(the_graph;tl(p)) path(the_graph;tl(p)) |
| THM | connect-iff | For any graph
( x,y:V. Dec(x = y)) x,y:V. Dec(x = y))   ( ( x,y:V. x-the_graph- > *y x,y:V. x-the_graph- > *y   x = y x = y 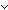 ( ( z:V. z:V.  z = x & x-the_graph- > z & z-the_graph- > *y)) z = x & x-the_graph- > z & z-the_graph- > *y)) |
| def | list-connect | L-G- > *x == ( y y L.y-G- > *x) L.y-G- > *x) |
| THM | list-connect-singleton | For any graph
 i,j:V. [i]-- > *j i,j:V. [i]-- > *j   i-the_graph- > *j i-the_graph- > *j |
| THM | list-connect-append | For any graph
 A,B:V List, i:V. A @ B-- > *i A,B:V List, i:V. A @ B-- > *i   A-- > *i A-- > *i 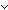 B-- > *i B-- > *i |
| def | list-list-connect | L1-G- > *L2 == ( x x L2.L1-G- > *x) L2.L1-G- > *x) |
| THM | list-list-connect_transitivity | For any graph
 A,B,C:V List. A-- > *B A,B,C:V List. A-- > *B   B-- > *C B-- > *C   A-- > *C A-- > *C |
| THM | list-list-connect-singleton | For any graph
 A:V List, x:V. A-- > *[x] A:V List, x:V. A-- > *[x]   A-- > *x A-- > *x |
| THM | list-list-connect-iseg | For any graph
 A,B:V List. B A,B:V List. B  A A   A-- > *B A-- > *B |
| THM | list-list-connect_weakening | For any graph
 A,B:V List. A = B A,B:V List. A = B   A-- > *B A-- > *B |
| THM | list-list-connect-append | For any graph
 A,B,C:V List. A-- > *B @ C A,B,C:V List. A-- > *B @ C   A-- > *B & A-- > *C A-- > *B & A-- > *C |
| THM | list-list-connect-append2 | For any graph
 A,B,C:V List. A-- > *C A,B,C:V List. A-- > *C 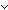 B-- > *C B-- > *C   A @ B-- > *C A @ B-- > *C |
| def | non-trivial-loop | non-trivial-loop(G;i) ==  j:Vertices(G). j:Vertices(G).  j = i & i-G- > *j & j-G- > *i j = i & i-G- > *j & j-G- > *i |
| def | non-trivial-loop-free | non-trivial-loop-free(G) ==  i:Vertices(G). i:Vertices(G).  non-trivial-loop(G;i) non-trivial-loop(G;i) |
| def | traversal | traversal(G) == (Vertices(G)+Vertices(G)) List |
| def | df-traversal | df-traversal(G;s) == ( i:Vertices(G), s1,s2:traversal(G). s = (s1 @ [inr(i)] @ s2) i:Vertices(G), s1,s2:traversal(G). s = (s1 @ [inr(i)] @ s2)  traversal(G) traversal(G)   ( ( j:Vertices(G). (inr(j) j:Vertices(G). (inr(j)  s2) s2)    (inl(j) (inl(j)  s2) s2)   j-G- > *i)) & ( j-G- > *i)) & ( i:Vertices(G), s1,s2:traversal(G). ( i:Vertices(G), s1,s2:traversal(G). ( j:Vertices(G). i-G- > *j j:Vertices(G). i-G- > *j    non-trivial-loop(G;j)) non-trivial-loop(G;j))   s = (s1 @ [inl(i)] @ s2) s = (s1 @ [inl(i)] @ s2)  traversal(G) traversal(G)   ( ( j:Vertices(G). i-G- > *j j:Vertices(G). i-G- > *j   (inr(j) (inr(j)  s2))) s2))) |
| THM | df-traversal-cons2 | For any graph
 i:V, s:Traversal. ( i:V, s:Traversal. ( j:V. (inr(j) j:V. (inr(j)  s) s)    (inl(j) (inl(j)  s) s)   j-the_graph- > *i) j-the_graph- > *i)   df-traversal(the_graph;s) df-traversal(the_graph;s)   df-traversal(the_graph;[inr(i) / s]) df-traversal(the_graph;[inr(i) / s]) |
| THM | df-traversal-nil | For any graph
df-traversal(the_graph;nil) |
| def | depthfirst-traversal | depthfirst-traversal(the_graph;s) ==  i:Vertices(the_graph), s1,s2:traversal(the_graph). ( i:Vertices(the_graph), s1,s2:traversal(the_graph). ( j:Vertices(the_graph). i-the_graph- > *j j:Vertices(the_graph). i-the_graph- > *j    non-trivial-loop(the_graph;j)) non-trivial-loop(the_graph;j))   s = (s1 @ [inl(i)] @ s2) s = (s1 @ [inl(i)] @ s2)  traversal(the_graph) traversal(the_graph)   ( ( j:Vertices(the_graph). j:Vertices(the_graph).  j = i j = i   i-the_graph- > *j i-the_graph- > *j   (inl(j) (inl(j)  s2)) s2)) |
| THM | paren-df-traversal |  G:Graph. ( G:Graph. ( x,y:Vertices(G). Dec(x = y)) x,y:Vertices(G). Dec(x = y))   ( ( s:traversal(G). paren(Vertices(G);s) s:traversal(G). paren(Vertices(G);s)   no_repeats(Vertices(G)+Vertices(G);s) no_repeats(Vertices(G)+Vertices(G);s)   df-traversal(G;s) df-traversal(G;s)   depthfirst-traversal(G;s)) depthfirst-traversal(G;s)) |
| def | topsorted | topsorted(the_graph;s) ==  i,j:Vertices(the_graph). i-the_graph- > *j i,j:Vertices(the_graph). i-the_graph- > *j    i = j i = j   i before j i before j  s s |
| def | dfl-traversal | dfl-traversal(the_graph;L;s) == ( i:Vertices(the_graph), s1,s2:traversal(the_graph). s = (s1 @ [inr(i)] @ s2) i:Vertices(the_graph), s1,s2:traversal(the_graph). s = (s1 @ [inr(i)] @ s2)  traversal(the_graph) traversal(the_graph)   ( ( j:Vertices(the_graph). (inr(j) j:Vertices(the_graph). (inr(j)  s2) s2)    (inl(j) (inl(j)  s2) s2)   j-the_graph- > *i)) & ( j-the_graph- > *i)) & ( j:Vertices(the_graph). (inr(j) j:Vertices(the_graph). (inr(j)  s) s)   L-the_graph- > *j) & ( L-the_graph- > *j) & ( i:Vertices(the_graph), s1,s2:traversal(the_graph). ( i:Vertices(the_graph), s1,s2:traversal(the_graph). ( j:Vertices(the_graph). i-the_graph- > *j j:Vertices(the_graph). i-the_graph- > *j    non-trivial-loop(the_graph;j)) non-trivial-loop(the_graph;j))   s = (s1 @ [inl(i)] @ s2) s = (s1 @ [inl(i)] @ s2)  traversal(the_graph) traversal(the_graph)   L-the_graph- > *i) L-the_graph- > *i) |
| THM | dfl-traversal-connect | For any graph
 L1,L2:V List, s:Traversal. L1-- > *L2 L1,L2:V List, s:Traversal. L1-- > *L2   dfl-traversal(the_graph;L2;s) dfl-traversal(the_graph;L2;s)   dfl-traversal(the_graph;L1;s) dfl-traversal(the_graph;L1;s) |
| THM | dfl-traversal-consr | For any graph
 L:V List, i:V, s:Traversal. ( L:V List, i:V, s:Traversal. ( j:V. (inr(j) j:V. (inr(j)  s) s)    (inl(j) (inl(j)  s) s)   j-the_graph- > *i) j-the_graph- > *i)   L-- > *i L-- > *i   dfl-traversal(the_graph;L;s) dfl-traversal(the_graph;L;s)   dfl-traversal(the_graph;L;[inr(i) / s]) dfl-traversal(the_graph;L;[inr(i) / s]) |
| THM | dfl-traversal-consl | For any graph
 L:V List, i:V, s:Traversal. (inr(i) L:V List, i:V, s:Traversal. (inr(i)  s) s)   dfl-traversal(the_graph;L;s) dfl-traversal(the_graph;L;s)   dfl-traversal(the_graph;L;[inl(i) / s]) dfl-traversal(the_graph;L;[inl(i) / s]) |
| def | dfsl-traversal | dfsl-traversal(the_graph;L;s) == df-traversal(the_graph;s) & ( i:Vertices(the_graph). (inl(i) i:Vertices(the_graph). (inl(i)  s) s)   L-the_graph- > *i) & (( L-the_graph- > *i) & (( i:Vertices(the_graph). L-the_graph- > *i i:Vertices(the_graph). L-the_graph- > *i    non-trivial-loop(the_graph;i)) non-trivial-loop(the_graph;i))   ( ( L1,L2:Vertices(the_graph) List. L = (L1 @ L2) L1,L2:Vertices(the_graph) List. L = (L1 @ L2)   ( ( s1,s2:traversal(the_graph). s = (s2 @ s1) s1,s2:traversal(the_graph). s = (s2 @ s1)  traversal(the_graph) & paren(Vertices(the_graph);s1) & paren(Vertices(the_graph);s2) & ( traversal(the_graph) & paren(Vertices(the_graph);s1) & paren(Vertices(the_graph);s2) & ( j:Vertices(the_graph). ((inl(j) j:Vertices(the_graph). ((inl(j)  s1) s1)   L1-the_graph- > *j) & ((inl(j) L1-the_graph- > *j) & ((inl(j)  s2) s2)   L2-the_graph- > *j & L2-the_graph- > *j &  L1-the_graph- > *j))))) L1-the_graph- > *j))))) |
| THM | dfsl-traversal-nil | For any graph
dfsl-traversal(the_graph;nil;nil) |
| THM | dfsl-traversal-append | For any graph
 L1,L2:V List, s:Traversal. L1-- > *L2 L1,L2:V List, s:Traversal. L1-- > *L2   dfsl-traversal(the_graph;L1;s) dfsl-traversal(the_graph;L1;s)   dfsl-traversal(the_graph;L1 @ L2;s) dfsl-traversal(the_graph;L1 @ L2;s) |
| def | topsortedl | topsortedl(the_graph;L;s) == ( i,j:Vertices(the_graph). i,j:Vertices(the_graph).  j = i j = i   i-the_graph- > *j i-the_graph- > *j   i before j i before j  s) & ( s) & ( i,j,k:Vertices(the_graph). k-the_graph- > *j i,j,k:Vertices(the_graph). k-the_graph- > *j    k-the_graph- > *i k-the_graph- > *i   ( ( k':Vertices(the_graph). k' before k k':Vertices(the_graph). k' before k  L L    k'-the_graph- > *i) k'-the_graph- > *i)   i before j i before j  s) s) |
| def | graph-isomorphic | G  H == H ==  vmap:(Vertices(G) vmap:(Vertices(G)  Vertices(H)), emap:(Edges(G) Vertices(H)), emap:(Edges(G)  Edges(H)). Bij(Vertices(G); Vertices(H); vmap) & Bij(Edges(G); Edges(H); emap) & (vmap,vmap) o Incidence(G) = Incidence(H) o emap Edges(H)). Bij(Vertices(G); Vertices(H); vmap) & Bij(Edges(G); Edges(H); emap) & (vmap,vmap) o Incidence(G) = Incidence(H) o emap |
| THM | graph-isomorphic_weakening |  G,H:Graph. G = H G,H:Graph. G = H   G G  H H |
| THM | graph-isomorphic_transitivity |  G,H,K:Graph. G G,H,K:Graph. G  H H   H H  K K   G G  K K |
| THM | graph-isomorphic_inversion |  G,H:Graph. G G,H:Graph. G  H H   H H  G G |
| THM | graph-isomorphic-equiv | EquivRel G,H:Graph. G  H H |
| def | rel-graph | Graph(x,y:T. R(x;y)) == < vertices = T, edges = {p:(T T)| R(1of(p);2of(p)) }, incidence = Id > T)| R(1of(p);2of(p)) }, incidence = Id > |
| THM | rel-graph_functionality |  R1,R2:(T R1,R2:(T  T T  Prop). ( Prop). ( x,y:T. R1(x,y) x,y:T. R1(x,y)   R2(x,y)) R2(x,y))   Graph(x,y:T. R1(x,y)) Graph(x,y:T. R1(x,y))  Graph(x,y:T. R2(x,y)) Graph(x,y:T. R2(x,y)) |
| def | fun-graph | Graph(a:A -- > f(a;b) | b:B) == < vertices = A, edges = A B, incidence = B, incidence = 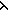 < a,b > . < a,f(a;b) > > < a,b > . < a,f(a;b) > > |
| def | divides-graph1 | DivGraph_1 == Graph(i,j:  . i | j) . i | j) |
| def | divides-graph2 | DivGraph_2 == Graph(i:  -- > i -- > i n | n: n | n:  ) ) |
| THM | fun-graph-rel-graph |  f:(A f:(A  B B  A). ( A). ( a:A, b1,b2:B. f(a,b1) = f(a,b2) a:A, b1,b2:B. f(a,b1) = f(a,b2)   b1 = b2) b1 = b2)   ( ( a,a':A. Dec( a,a':A. Dec( b:B. a' = f(a,b))) b:B. a' = f(a,b)))   Graph(a:A -- > f(a,b) | b:B) Graph(a:A -- > f(a,b) | b:B)  Graph(a,a':A. Graph(a,a':A.  b:B. a' = f(a,b)) b:B. a' = f(a,b)) |
| THM | div-graph-iso | DivGraph_2  DivGraph_1 DivGraph_1 |