| 1 | 1. T: Type
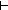 no_repeats(T+T;nil) no_repeats(T+T;nil)   ( ( s1,s2,s3:(T+T) List, x:T. nil = (s1 @ [inl(x)] @ s2 @ [inr(x)] @ s3) s1,s2,s3:(T+T) List, x:T. nil = (s1 @ [inl(x)] @ s2 @ [inr(x)] @ s3)   paren(T;s2)) paren(T;s2)) | 1 step |
| |
| 2 | 1. T: Type
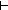  s1,s2:(T+T) List. (no_repeats(T+T;s1) s1,s2:(T+T) List. (no_repeats(T+T;s1)   ( ( s1@0,s2,s3:(T+T) List, x:T. s1 = (s1@0 @ [inl(x)] @ s2 @ [inr(x)] @ s3) s1@0,s2,s3:(T+T) List, x:T. s1 = (s1@0 @ [inl(x)] @ s2 @ [inr(x)] @ s3)   paren(T;s2))) paren(T;s2)))   (no_repeats(T+T;s2) (no_repeats(T+T;s2)   ( ( s1,s2@0,s3:(T+T) List, x:T. s2 = (s1 @ [inl(x)] @ s2@0 @ [inr(x)] @ s3) s1,s2@0,s3:(T+T) List, x:T. s2 = (s1 @ [inl(x)] @ s2@0 @ [inr(x)] @ s3)   paren(T;s2@0))) paren(T;s2@0)))   paren(T;s1) paren(T;s1)   paren(T;s2) paren(T;s2)   no_repeats(T+T;s1 @ s2) no_repeats(T+T;s1 @ s2)   ( ( s1@0,s2@0,s3:(T+T) List, x:T. (s1 @ s2) = (s1@0 @ [inl(x)] @ s2@0 @ [inr(x)] @ s3) s1@0,s2@0,s3:(T+T) List, x:T. (s1 @ s2) = (s1@0 @ [inl(x)] @ s2@0 @ [inr(x)] @ s3)   paren(T;s2@0)) paren(T;s2@0)) | 31 steps |
| |
| 3 | 1. T: Type
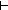  s:(T+T) List, t:T. (no_repeats(T+T;s) s:(T+T) List, t:T. (no_repeats(T+T;s)   ( ( s1,s2,s3:(T+T) List, x:T. s = (s1 @ [inl(x)] @ s2 @ [inr(x)] @ s3) s1,s2,s3:(T+T) List, x:T. s = (s1 @ [inl(x)] @ s2 @ [inr(x)] @ s3)   paren(T;s2))) paren(T;s2)))   paren(T;s) paren(T;s)   no_repeats(T+T;[inl(t)] @ s @ [inr(t)]) no_repeats(T+T;[inl(t)] @ s @ [inr(t)])   ( ( s1,s2,s3:(T+T) List, x:T. ([inl(t)] @ s @ [inr(t)]) = (s1 @ [inl(x)] @ s2 @ [inr(x)] @ s3) s1,s2,s3:(T+T) List, x:T. ([inl(t)] @ s @ [inr(t)]) = (s1 @ [inl(x)] @ s2 @ [inr(x)] @ s3)   paren(T;s2)) paren(T;s2)) | 27 steps |