| 1 | 1. A: Type
2. B: Type
3. f: A  B B  A A
4.  a:A, b1,b2:B. f(a,b1) = f(a,b2) a:A, b1,b2:B. f(a,b1) = f(a,b2)   b1 = b2 b1 = b2
5.  a,a':A. Dec( a,a':A. Dec( b:B. a' = f(a,b)) b:B. a' = f(a,b))
6. p: A B B
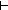 < 1of(p),f(1of(p),2of(p)) > < 1of(p),f(1of(p),2of(p)) >  {p:(A {p:(A A)| A)|  b:B. 2of(p) = f(1of(p),b) b:B. 2of(p) = f(1of(p),b)  A } A } | 1 step |
| |
| 2 | 1. A: Type
2. B: Type
3. f: A  B B  A A
4.  a:A, b1,b2:B. f(a,b1) = f(a,b2) a:A, b1,b2:B. f(a,b1) = f(a,b2)   b1 = b2 b1 = b2
5.  a,a':A. Dec( a,a':A. Dec( b:B. a' = f(a,b)) b:B. a' = f(a,b))
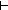 Bij(A; A; Id) Bij(A; A; Id) | 1 step |
| |
| 3 | 1. A: Type
2. B: Type
3. f: A  B B  A A
4.  a:A, b1,b2:B. f(a,b1) = f(a,b2) a:A, b1,b2:B. f(a,b1) = f(a,b2)   b1 = b2 b1 = b2
5.  a,a':A. Dec( a,a':A. Dec( b:B. a' = f(a,b)) b:B. a' = f(a,b))
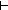 Bij(A Bij(A B; {p:(A B; {p:(A A)| A)|  b:B. 2of(p) = f(1of(p),b) b:B. 2of(p) = f(1of(p),b)  A }; A }; 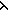 p. < 1of(p),f(1of(p),2of(p)) > ) p. < 1of(p),f(1of(p),2of(p)) > ) | 10 steps |
| |
| 4 | 1. A: Type
2. B: Type
3. f: A  B B  A A
4.  a:A, b1,b2:B. f(a,b1) = f(a,b2) a:A, b1,b2:B. f(a,b1) = f(a,b2)   b1 = b2 b1 = b2
5.  a,a':A. Dec( a,a':A. Dec( b:B. a' = f(a,b)) b:B. a' = f(a,b))
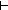 (Id,Id) o (Id,Id) o 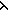 p. < 1of(p),f(1of(p),2of(p)) > = Id o ( p. < 1of(p),f(1of(p),2of(p)) > = Id o (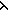 p. < 1of(p),f(1of(p),2of(p)) > ) p. < 1of(p),f(1of(p),2of(p)) > )  A A B B  A A A A | 1 step |