| Rank | Theorem | Name |
| 4 | Thm*  r,k: r,k: , L,R: , L,R: List. 2 List. 2 k k   ||R|| = ||L|| ||R|| = ||L||     ( ( i: i: ||L||. 0 < L[i] ||L||. 0 < L[i]   R[i]- > L[i--]^k) R[i]- > L[i--]^k)   r- > R^k-1 r- > R^k-1   r+1- > L^k r+1- > L^k | [Ramsey-recursion] |
| cites |
| 0 | Thm*  as,bs:T List. ||as @ bs|| = ||as||+||bs|| as,bs:T List. ||as @ bs|| = ||as||+||bs||   | [length_append] |
| 1 | Thm*  as,bs:T List, i:{||as||..(||as||+||bs||) as,bs:T List, i:{||as||..(||as||+||bs||) }. (as @ bs)[i] = bs[(i-||as||)] }. (as @ bs)[i] = bs[(i-||as||)] | [select_append_back] |
| 1 | Thm*  as,bs:T List, i: as,bs:T List, i: ||as||. (as @ bs)[i] = as[i] ||as||. (as @ bs)[i] = as[i] | [select_append_front] |
| 2 | Thm*  L: L: List, i: List, i: ||L||. 0 < L[i] ||L||. 0 < L[i]   ||L[i--]|| = ||L|| ||L[i--]|| = ||L||   | [list-dec-length] |
| 0 | Thm*  n,m: n,m:  , f:( , f:( (n-1) (n-1)   (m-1)). increasing(f;n-1) (m-1)). increasing(f;n-1)   increasing(f[n-1:=m-1];n) increasing(f[n-1:=m-1];n) | [fappend-increasing] |
| 0 | Thm*  a:T, as:T List, i: a:T, as:T List, i: . 0 < i . 0 < i   i i ||as|| ||as||   [a / as][i] = as[(i-1)] [a / as][i] = as[(i-1)] | [select_cons_tl] |
| 0 | Thm*  as:A List, n:{0...||as||}. ||firstn(n;as)|| = n as:A List, n:{0...||as||}. ||firstn(n;as)|| = n   | [length_firstn] |
| 0 | Thm*  s:T List. 0 < ||s|| s:T List. 0 < ||s||   (s ~ (firstn(||s||-1;s) @ [s[(||s||-1)]])) (s ~ (firstn(||s||-1;s) @ [s[(||s||-1)]])) | [list-decomp-last] |
| 0 | Thm*  f,as':Top, A:Type, as:A List. map(f;as @ as') ~ (map(f;as) @ map(f;as')) f,as':Top, A:Type, as:A List. map(f;as @ as') ~ (map(f;as) @ map(f;as')) | [map_append_sq] |
| 1 | Thm*  as:T List, n:{0...||as||}, i: as:T List, n:{0...||as||}, i: n. firstn(n;as)[i] = as[i] n. firstn(n;as)[i] = as[i] | [select_firstn] |
| 3 | Thm*  L: L: List, i,j: List, i,j: ||L||. 0 < L[i] ||L||. 0 < L[i]   L[i--][j] = if j= L[i--][j] = if j=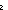 i i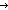 L[j]-1 else L[j] fi L[j]-1 else L[j] fi | [list-dec-select] |
| 1 | Thm*  k,m: k,m: , f:( , f:( k k   m), g:( m), g:( m m   ). increasing(f;k) ). increasing(f;k)   increasing(g;m) increasing(g;m)   increasing(g o f;k) increasing(g o f;k) | [compose_increasing] |
| 0 | Thm*  f,g:Top, s:Top List. map(f;map(g;s)) ~ map(f o g;s) f,g:Top, s:Top List. map(f;map(g;s)) ~ map(f o g;s) | [map-map] |
| 1 | Thm*  f:(A f:(A  B), as:A List, n: B), as:A List, n: ||as||. map(f;as)[n] = f(as[n]) ||as||. map(f;as)[n] = f(as[n]) | [map_select] |
| 0 | Thm*  f:(A f:(A  B), as:A List. ||map(f;as)|| = ||as|| B), as:A List. ||map(f;as)|| = ||as||   | [map_length] |
| 0 | Thm*  k: k: , f:( , f:( k k   ). increasing(f;k) ). increasing(f;k)   ( ( x,y: x,y: k. x < y k. x < y   f(x) < f(y)) f(x) < f(y)) | [increasing_implies] |