| Rank | Theorem | Name |
| 3 | Thm*  n,k: n,k: , c:( , c:( n n   k). k).  p:( p:( k k  ( ( List)). sum(||p(j)|| | j < k) = n & ( List)). sum(||p(j)|| | j < k) = n & ( j: j: k, x,y: k, x,y: ||p(j)||. x < y ||p(j)||. x < y   (p(j))[x] > (p(j))[y]) & ( (p(j))[x] > (p(j))[y]) & ( j: j: k, x: k, x: ||p(j)||. (p(j))[x] < n & c((p(j))[x]) = j) ||p(j)||. (p(j))[x] < n & c((p(j))[x]) = j) | [finite-partition] |
| cites |
| 0 | Thm*  n: n: , a: , a: . sum(a | x < n) = a . sum(a | x < n) = a n n | [sum_constant] |
| 0 | Thm*  n: n: , f,g:( , f,g:( n n   ). ( ). ( i: i: n. f(i) = g(i)) n. f(i) = g(i))   sum(f(x) | x < n) = sum(g(x) | x < n) sum(f(x) | x < n) = sum(g(x) | x < n) | [sum_functionality] |
| 0 | Thm*  k: k: , f,g:( , f,g:( k k   ), p:( ), p:( k k  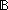 ). sum(if p(i) ). sum(if p(i)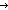 f(i)+g(i) else f(i) fi | i < k) = sum(f(i) | i < k)+sum(if p(i) f(i)+g(i) else f(i) fi | i < k) = sum(f(i) | i < k)+sum(if p(i)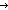 g(i) else 0 fi | i < k) g(i) else 0 fi | i < k) | [sum-ite] |
| 2 | Thm*  n: n: , f:( , f:( n n   ), m: ), m: n. ( n. ( x: x: n. n.  x = m x = m   f(x) = 0) f(x) = 0)   sum(f(x) | x < n) = f(m) sum(f(x) | x < n) = f(m) | [singleton_support_sum] |
| 0 | Thm*  a:T, as:T List, i: a:T, as:T List, i: . 0 < i . 0 < i   i i ||as|| ||as||   [a / as][i] = as[(i-1)] [a / as][i] = as[(i-1)] | [select_cons_tl] |