| Rank | Theorem | Name |
| 2 | Thm*  s:(T+T) List. paren(T;s)   (i:T, s1,s2:(T+T) List. s = (s1 @ [inl(i)] @ s2) (inr(i)  s2)) | [paren_order1] |
| cites |
| 1 | Thm* P:(((T+T) List)  Prop). P(nil) (s1,s2:(T+T) List. P(s1) P(s2) paren(T;s1) paren(T;s2) P(s1 @ s2)) (s:(T+T) List, t:T. P(s) paren(T;s) P([inl(t)] @ s @ [inr(t)])) (s:(T+T) List. paren(T;s) P(s)) | [paren_induction] |
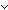| 0 | Thm* a,c,b,d:T List. (a @ b) = (c @ d) ( e:T List. a = (c @ e) & d = (e @ b)  c = (a @ e) & b = (e @ d)) | [equal_appends] |
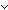| 0 | Thm* a,b:T List, x:T. [x] = (a @ b) a = nil & b = [x] b = nil & a = [x] | [append_is_singleton] |