| Rank | Theorem | Name |
| 5 | Thm*  p: p:  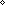 . prime(p) . prime(p)   ( ( m,n: m,n: . m . m m = p m = p n n n n   n = 0) n = 0) | [sqrt_prime_irrational] |
| cites |
| 2 | Thm*  a: a: , n: , n:  . a = (a . a = (a 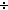 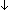 n) n) n+(a mod n) & (a mod n) < n n+(a mod n) & (a mod n) < n | [div_floor_mod_properties] |
| 0 | Thm*  a,b: a,b: . a . a b = b b = b a a | [mul_com] |
| 0 | Thm*  a,b: a,b: , n: , n: . a . a b b   n n a a n n b b | [mul_preserves_le] |
| 1 | Thm*  a,b: a,b: , n: , n:  . n . n a < n a < n b b   a < b a < b | [mul_cancel_in_lt] |
| 3 | Thm*  a,b: a,b: , n: , n:  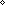 . n . n a = n a = n b b   a = b a = b | [mul_cancel_in_eq] |
| 2 | Thm*  a,b: a,b:  . 0 < a . 0 < a b b | [mul_bounds_1b] |
| 4 | Thm*  a,b: a,b: . a . a b < 0 b < 0   a < 0 & b > 0 a < 0 & b > 0 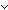 a > 0 & b < 0 a > 0 & b < 0 | [neg_mul_arg_bounds] |
| 3 | Thm*  a,b: a,b: . a . a b > 0 b > 0   a > 0 & b > 0 a > 0 & b > 0 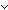 a < 0 & b < 0 a < 0 & b < 0 | [pos_mul_arg_bounds] |
| 1 | Thm*  a,b: a,b: . 0 . 0 a a b b | [mul_bounds_1a] |