| Rank | Theorem | Name |
| 3 | Thm*  M:AdjMatrix, T:Type, s:T, x:Vertices(adjm-graph(M)), f:(T  Vertices(adjm-graph(M))T).  L:Vertices(adjm-graph(M)) List. (y:Vertices(adjm-graph(M)). x-adjm-graph(M)- > y   (y  L)) & adjm-edge-accum(M;s',x'.f(s',x');s;x) = list_accum(s',x'.f(s',x');s;L) | [adjm-edge-accum-properties] |
| cites |
| 2 | Thm* P:(T 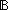), L:T List, x:T. (x filter(P;L)) (x L) & P(x) | [member_filter] |
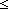| 2 | Thm* i,j,k: . (k upto(i;j)) i k & k < j | [member_upto] |
| 0 | Thm* f:(TAT), P:(A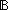), L:A List, s:T. list_accum(s',x'.f(s',x');s;filter(P;L)) ~ list_accum(i,y.if P(y)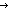 f(i,y) else i fi;s;L) | [list_accum_filter] |
| 0 | Thm* n:, f,x:Top. primrec(n;x;f) ~ list_accum(i,y.f(y,i);x;upto(0;n)) | [primrec_list_accum] |