Selected Objects
| def | graphobj | GraphObject(the_graph) == eq:Vertices(the_graph)  Vertices(the_graph) Vertices(the_graph)  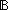  ( ( x,y:Vertices(the_graph). eq(x,y) x,y:Vertices(the_graph). eq(x,y)   x = y) x = y) (eacc:( (eacc:(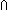 T:Type. (T T:Type. (T  Vertices(the_graph) Vertices(the_graph)  T) T)  T T  Vertices(the_graph) Vertices(the_graph)  T) T) ( ( T:Type, s:T, x:Vertices(the_graph), f:(T T:Type, s:T, x:Vertices(the_graph), f:(T  Vertices(the_graph) Vertices(the_graph)  T). T).  L:Vertices(the_graph) List. ( L:Vertices(the_graph) List. ( y:Vertices(the_graph). x-the_graph- > y y:Vertices(the_graph). x-the_graph- > y   (y (y  L)) & eacc(f,s,x) = list_accum(s',x'.f(s',x');s;L)) L)) & eacc(f,s,x) = list_accum(s',x'.f(s',x');s;L)) (vacc:( (vacc:(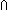 T:Type. (T T:Type. (T  Vertices(the_graph) Vertices(the_graph)  T) T)  T T  T) T) ( ( T:Type, s:T, f:(T T:Type, s:T, f:(T  Vertices(the_graph) Vertices(the_graph)  T). T).  L:Vertices(the_graph) List. no_repeats(Vertices(the_graph);L) & ( L:Vertices(the_graph) List. no_repeats(Vertices(the_graph);L) & ( y:Vertices(the_graph). (y y:Vertices(the_graph). (y  L)) & vacc(f,s) = list_accum(s',x'.f(s',x');s;L)) L)) & vacc(f,s) = list_accum(s',x'.f(s',x');s;L)) Top)) Top)) |
| def | gro_eq | t.eq == 1of(t) |
| def | gro_eqw | t.eqw == 1of(2of(t)) |
| def | gro_eacc | t.eacc == 1of(2of(2of(t))) |
| def | gro_eaccw | t.eaccw == 1of(2of(2of(2of(t)))) |
| def | gro_vacc | t.vacc == 1of(2of(2of(2of(2of(t))))) |
| def | gro_vaccw | t.vaccw == 1of(2of(2of(2of(2of(2of(t)))))) |
| def | gro_other | t.other == 2of(2of(2of(2of(2of(2of(t)))))) |
| def | mkgraphobj | mkgraphobj(eq, eqw, eacc, eaccw, vacc, vaccw, other) == < eq,eqw,eacc,eaccw,vacc,vaccw,other > |
| def | graphrep | Graph Representation == type:Type graph:type graph:type  Graph Graph r:type r:type  GraphObject(graph(r)) GraphObject(graph(r)) |
| def | grr_type | t.type == 1of(t) |
| def | grr_graph | t.graph == 1of(2of(t)) |
| def | grr_obj | t.obj == 2of(2of(t)) |
| def | mkgraphrep | mkgraphrep(type, graph, obj) == < type,graph,obj > |
| THM | graphobj-properties | For any graph
 the_obj:GraphObject(the_graph). ( the_obj:GraphObject(the_graph). ( x,y:V. the_obj.eq(x,y) x,y:V. the_obj.eq(x,y)   x = y) & ( x = y) & ( T:Type, s:T, x:V, f:(T T:Type, s:T, x:V, f:(T  V V  T). T).  L:V List. ( L:V List. ( y:V. x-the_graph- > y y:V. x-the_graph- > y   (y (y  L)) & the_obj.eacc(f,s,x) = list_accum(s',x'.f(s',x');s;L)) & ( L)) & the_obj.eacc(f,s,x) = list_accum(s',x'.f(s',x');s;L)) & ( T:Type, s:T, f:(T T:Type, s:T, f:(T  V V  T). T).  L:V List. no_repeats(V;L) & ( L:V List. no_repeats(V;L) & ( y:V. (y y:V. (y  L)) & the_obj.vacc(f,s) = list_accum(s',x'.f(s',x');s;L)) L)) & the_obj.vacc(f,s) = list_accum(s',x'.f(s',x');s;L)) |
| def | vertex-subset | vertex-subset(the_obj;x.P(x)) == the_obj.vacc(( l,x. if P(x) l,x. if P(x)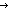 [x / l] else l fi),nil) [x / l] else l fi),nil) |
| THM | vertex-subset-properties | For any graph
 the_obj:GraphObject(the_graph), P:(V the_obj:GraphObject(the_graph), P:(V  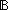 ). no_repeats(V;vertex-subset(the_obj;x.P(x))) & ( ). no_repeats(V;vertex-subset(the_obj;x.P(x))) & ( x:V. (x x:V. (x  vertex-subset(the_obj;x.P(x))) vertex-subset(the_obj;x.P(x)))   P(x)) P(x)) |
| def | vertex-count | vertex-count(the_obj;x.P(x)) == ||vertex-subset(the_obj;x.P(x))|| |
| THM | vertex-count-le | For any graph
 the_obj:GraphObject(the_graph), P,Q:(V the_obj:GraphObject(the_graph), P,Q:(V  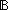 ). ( ). ( x:V. P(x) x:V. P(x)   Q(x)) Q(x))   vertex-count(the_obj;x.P(x)) vertex-count(the_obj;x.P(x))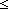 vertex-count(the_obj;x.Q(x)) vertex-count(the_obj;x.Q(x)) |
| THM | vertex-count-less | For any graph
 the_obj:GraphObject(the_graph), P,Q:(V the_obj:GraphObject(the_graph), P,Q:(V  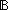 ). ( ). ( x:V. P(x) x:V. P(x)   Q(x)) Q(x))   ( ( x:V. x:V.  P(x) & Q(x)) P(x) & Q(x))   vertex-count(the_obj;x.P(x)) < vertex-count(the_obj;x.Q(x)) vertex-count(the_obj;x.P(x)) < vertex-count(the_obj;x.Q(x)) |
| def | allgrep | For any graph representationP(the_graph;the_obj) ==  R:Graph Representation, r:R.type. P(R.graph(r);R.obj(r)) R:Graph Representation, r:R.type. P(R.graph(r);R.obj(r)) |
| THM | decidable__equal_gr_v | For any graph
 the_obj:GraphObject(the_graph), x,y:V. Dec(x = y) the_obj:GraphObject(the_graph), x,y:V. Dec(x = y) |
| THM | dfs-measure | For any graph
 the_obj:GraphObject(the_graph). the_obj:GraphObject(the_graph).  M:(Traversal M:(Traversal   ). ( ). ( i:V, s:Traversal. M([inl(i) / s]) i:V, s:Traversal. M([inl(i) / s])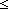 M(s)) & ( M(s)) & ( i:V, s:Traversal. i:V, s:Traversal.  member-paren(x,y.the_obj.eq(x,y);i;s) member-paren(x,y.the_obj.eq(x,y);i;s)   M([inr(i) / s]) < M(s)) M([inr(i) / s]) < M(s)) |
| def | dfs | (rec) dfs(the_obj;s;i) == if member-paren(x,y.the_obj.eq(x,y);i;s)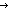 s else [inl(i) / (the_obj.eacc(( s else [inl(i) / (the_obj.eacc(( s',j. dfs(the_obj;s';j)),[inr(i) / s],i))] fi s',j. dfs(the_obj;s';j)),[inr(i) / s],i))] fi |
| THM | dfs_induction | For any graph
 the_obj:GraphObject(the_graph), P:(V the_obj:GraphObject(the_graph), P:(V  Traversal Traversal  Traversal Traversal  Prop), s:Traversal, i:V. ( Prop), s:Traversal, i:V. ( s1,s2:Traversal, i:V. P(i,s1,s2) s1,s2:Traversal, i:V. P(i,s1,s2)   l_disjoint(V+V;s2;s1) & no_repeats(V+V;s2)) l_disjoint(V+V;s2;s1) & no_repeats(V+V;s2))   ( ( s:Traversal, i:V. member-paren(x,y.the_obj.eq(x,y);i;s) s:Traversal, i:V. member-paren(x,y.the_obj.eq(x,y);i;s)   P(i,s,nil)) P(i,s,nil))   ( ( s1,s2,s3:Traversal, i,j:V. i-the_graph- > j s1,s2,s3:Traversal, i,j:V. i-the_graph- > j   P(j,s1,s2) P(j,s1,s2)   P(i,s2 @ s1,s3) P(i,s2 @ s1,s3)   P(i,s1,s3 @ s2)) P(i,s1,s3 @ s2))   ( ( s1,s2:Traversal, i:V. s1,s2:Traversal, i:V.  member-paren(x,y.the_obj.eq(x,y);i;s1) member-paren(x,y.the_obj.eq(x,y);i;s1)   P(i,[inr(i) / s1],s2) P(i,[inr(i) / s1],s2)   P(i,s1,[inl(i) / (s2 @ [inr(i)])])) P(i,s1,[inl(i) / (s2 @ [inr(i)])]))   ( ( s':Traversal. P(i,s,s') & dfs(the_obj;s;i) = (s' @ s)) s':Traversal. P(i,s,s') & dfs(the_obj;s;i) = (s' @ s)) |
| THM | dfs_induction2 | For any graph
 the_obj:GraphObject(the_graph), P:(V the_obj:GraphObject(the_graph), P:(V  Traversal Traversal  Traversal Traversal  Prop), s:Traversal, i:V. ( Prop), s:Traversal, i:V. ( s:Traversal, i:V. (inl(i) s:Traversal, i:V. (inl(i)  s) s) 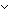 (inr(i) (inr(i)  s) s)   P(i,s,nil)) P(i,s,nil))   ( ( s1,s2,s3:Traversal, i,j:V. i-the_graph- > j s1,s2,s3:Traversal, i,j:V. i-the_graph- > j   paren(V;s2) paren(V;s2)   paren(V;s3) paren(V;s3)   P(j,s1,s2) P(j,s1,s2)   P(i,s2 @ s1,s3) P(i,s2 @ s1,s3)   P(i,s1,s3 @ s2)) P(i,s1,s3 @ s2))   ( ( s1,s2:Traversal, i:V. s1,s2:Traversal, i:V.  (inl(i) (inl(i)  s1) s1)    (inr(i) (inr(i)  s1) s1)   P(i,[inr(i) / s1],s2) P(i,[inr(i) / s1],s2)   P(i,s1,[inl(i) / (s2 @ [inr(i)])])) P(i,s1,[inl(i) / (s2 @ [inr(i)])]))   ( ( s':Traversal. P(i,s,s') & l_disjoint(V+V;s';s) & no_repeats(V+V;s') & paren(V;s') & dfs(the_obj;s;i) = (s' @ s)) s':Traversal. P(i,s,s') & l_disjoint(V+V;s';s) & no_repeats(V+V;s') & paren(V;s') & dfs(the_obj;s;i) = (s' @ s)) |
| THM | dfs_member | For any graph
 the_obj:GraphObject(the_graph), s:Traversal, i:V. the_obj:GraphObject(the_graph), s:Traversal, i:V.  s':Traversal. (inl(i) s':Traversal. (inl(i)  s') s') 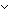 (inl(i) (inl(i)  s) s) 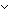 (inr(i) (inr(i)  s) & l_disjoint(V+V;s';s) & no_repeats(V+V;s') & paren(V;s') & dfs(the_obj;s;i) = (s' @ s) s) & l_disjoint(V+V;s';s) & no_repeats(V+V;s') & paren(V;s') & dfs(the_obj;s;i) = (s' @ s) |
| THM | dfs_accum_member | For any graph
 the_obj:GraphObject(the_graph), l:V List, s:Traversal. the_obj:GraphObject(the_graph), l:V List, s:Traversal.  s':Traversal. ( s':Traversal. ( i:V. (i i:V. (i  l) l)   (inl(i) (inl(i)  s') s') 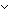 (inl(i) (inl(i)  s) s) 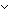 (inr(i) (inr(i)  s)) & l_disjoint(V+V;s';s) & no_repeats(V+V;s') & paren(V;s') & list_accum(s',j.dfs(the_obj;s';j);s;l) = (s' @ s) s)) & l_disjoint(V+V;s';s) & no_repeats(V+V;s') & paren(V;s') & list_accum(s',j.dfs(the_obj;s';j);s;l) = (s' @ s) |
| THM | dfs_induction3 | For any graph
 the_obj:GraphObject(the_graph), P:(V the_obj:GraphObject(the_graph), P:(V  Traversal Traversal  Traversal Traversal  Prop), s:Traversal, i:V. ( Prop), s:Traversal, i:V. ( s1,s2:Traversal, i:V. P(i,s1,s2) s1,s2:Traversal, i:V. P(i,s1,s2)   l_disjoint(V+V;s2;s1) & no_repeats(V+V;s2)) l_disjoint(V+V;s2;s1) & no_repeats(V+V;s2))   ( ( s:Traversal, i:V. member-paren(x,y.the_obj.eq(x,y);i;s) s:Traversal, i:V. member-paren(x,y.the_obj.eq(x,y);i;s)   P(i,s,nil)) P(i,s,nil))   ( ( s1,s2,s3:Traversal, i,j:V. i-the_graph- > j s1,s2,s3:Traversal, i,j:V. i-the_graph- > j   P(j,s1,s2) P(j,s1,s2)   P(i,s2 @ s1,s3) P(i,s2 @ s1,s3)   P(i,s1,s3 @ s2)) P(i,s1,s3 @ s2))   ( ( s1,s2:Traversal, i:V. s1,s2:Traversal, i:V.  member-paren(x,y.the_obj.eq(x,y);i;s1) member-paren(x,y.the_obj.eq(x,y);i;s1)   ( ( j:V. i-the_graph- > j j:V. i-the_graph- > j    j = i j = i   (inl(j) (inl(j)  s2) s2) 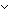 member-paren(x,y.the_obj.eq(x,y);j;s1)) member-paren(x,y.the_obj.eq(x,y);j;s1))   P(i,[inr(i) / s1],s2) P(i,[inr(i) / s1],s2)   P(i,s1,[inl(i) / (s2 @ [inr(i)])])) P(i,s1,[inl(i) / (s2 @ [inr(i)])]))   ( ( s':Traversal. P(i,s,s') & dfs(the_obj;s;i) = (s' @ s)) s':Traversal. P(i,s,s') & dfs(the_obj;s;i) = (s' @ s)) |
| THM | dfs-cases | For any graph
 the_obj:GraphObject(the_graph), s:Traversal, i:V. the_obj:GraphObject(the_graph), s:Traversal, i:V.  s':Traversal. ((inr(i) s':Traversal. ((inr(i)  s) s) 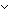 (inl(i) (inl(i)  s) s)   s' = nil) & ( s' = nil) & ( (inr(i) (inr(i)  s) & s) &  (inl(i) (inl(i)  s) s)   ( ( s2:Traversal. s' = ([inl(i)] @ s2 @ [inr(i)]) s2:Traversal. s' = ([inl(i)] @ s2 @ [inr(i)])  Traversal)) & dfs(the_obj;s;i) = (s' @ s) Traversal)) & dfs(the_obj;s;i) = (s' @ s) |
| THM | dfs-connect | For any graph
 the_obj:GraphObject(the_graph), s:Traversal, i:V. the_obj:GraphObject(the_graph), s:Traversal, i:V.  s':Traversal. ( s':Traversal. ( j:V. (inr(j) j:V. (inr(j)  s') s')   i-the_graph- > *j) & dfs(the_obj;s;i) = (s' @ s) i-the_graph- > *j) & dfs(the_obj;s;i) = (s' @ s) |
| THM | dfs-properties | For any graph
 the_obj:GraphObject(the_graph), s:Traversal, i:V. the_obj:GraphObject(the_graph), s:Traversal, i:V.  s':Traversal. ((inr(i) s':Traversal. ((inr(i)  s) s) 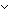 (inl(i) (inl(i)  s) s)   s' = nil) & ( s' = nil) & ( (inr(i) (inr(i)  s) & s) &  (inl(i) (inl(i)  s) s)   ( ( s2:Traversal. s' = ([inl(i)] @ s2 @ [inr(i)]) s2:Traversal. s' = ([inl(i)] @ s2 @ [inr(i)])  Traversal)) & l_disjoint(V+V;s';s) & no_repeats(V+V;s') & paren(V;s') & ( Traversal)) & l_disjoint(V+V;s';s) & no_repeats(V+V;s') & paren(V;s') & ( j:V. (inr(j) j:V. (inr(j)  s') s')   i-the_graph- > *j) & dfs(the_obj;s;i) = (s' @ s) i-the_graph- > *j) & dfs(the_obj;s;i) = (s' @ s) |
| THM | dfs_induction4 | For any graph
 the_obj:GraphObject(the_graph), P:(V the_obj:GraphObject(the_graph), P:(V  Traversal Traversal  Traversal Traversal  Prop), s:Traversal, i:V. ( Prop), s:Traversal, i:V. ( s:Traversal, i:V. (inl(i) s:Traversal, i:V. (inl(i)  s) s) 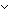 (inr(i) (inr(i)  s) s)   P(i,s,nil)) P(i,s,nil))   ( ( s1,s2,s3:Traversal, i,j:V. i-the_graph- > j s1,s2,s3:Traversal, i,j:V. i-the_graph- > j   paren(V;s2) paren(V;s2)   ( ( k:V. (inr(k) k:V. (inr(k)  s2) s2)   j-the_graph- > *k) j-the_graph- > *k)   paren(V;s3) paren(V;s3)   P(j,s1,s2) P(j,s1,s2)   P(i,s2 @ s1,s3) P(i,s2 @ s1,s3)   P(i,s1,s3 @ s2)) P(i,s1,s3 @ s2))   ( ( s1,s2:Traversal, i:V. s1,s2:Traversal, i:V.  (inr(i) (inr(i)  s1) s1)    (inl(i) (inl(i)  s1) s1)   paren(V;s2) paren(V;s2)   l_disjoint(V+V;s2;s1) l_disjoint(V+V;s2;s1)   no_repeats(V+V;s2) no_repeats(V+V;s2)   ( ( j:V. (inr(j) j:V. (inr(j)  s2) s2)   i-the_graph- > *j) i-the_graph- > *j)   ( ( j:V. i-the_graph- > j j:V. i-the_graph- > j    j = i j = i   (inl(j) (inl(j)  s2) s2) 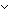 (inl(j) (inl(j)  s1) s1) 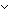 (inr(j) (inr(j)  s1)) s1))   P(i,[inr(i) / s1],s2) P(i,[inr(i) / s1],s2)   P(i,s1,[inl(i) / (s2 @ [inr(i)])])) P(i,s1,[inl(i) / (s2 @ [inr(i)])]))   ( ( s':Traversal. P(i,s,s') & l_disjoint(V+V;s';s) & no_repeats(V+V;s') & paren(V;s') & ( s':Traversal. P(i,s,s') & l_disjoint(V+V;s';s) & no_repeats(V+V;s') & paren(V;s') & ( j:V. (inr(j) j:V. (inr(j)  s') s')   i-the_graph- > *j) & dfs(the_obj;s;i) = (s' @ s)) i-the_graph- > *j) & dfs(the_obj;s;i) = (s' @ s)) |
| THM | dfs-df-traversal | For any graph
 the_obj:GraphObject(the_graph), s:Traversal, i:V. df-traversal(the_graph;s) the_obj:GraphObject(the_graph), s:Traversal, i:V. df-traversal(the_graph;s)   ( ( j:V. (inr(j) j:V. (inr(j)  s) s)    (inl(j) (inl(j)  s) s)   j-the_graph- > *i) j-the_graph- > *i)   df-traversal(the_graph;dfs(the_obj;s;i)) df-traversal(the_graph;dfs(the_obj;s;i)) |
| def | depthfirst | depthfirst(the_obj) == the_obj.vacc(( s,i. dfs(the_obj;s;i)),nil) s,i. dfs(the_obj;s;i)),nil) |
| def | dfsl | dfsl(G;L) == list_accum(s,i.dfs(G;s;i);nil;L) |
| THM | dfsl-induction1 | For any graph
 the_obj:GraphObject(the_graph), P:((V List) the_obj:GraphObject(the_graph), P:((V List)  Traversal Traversal  Prop). P(nil,nil) Prop). P(nil,nil)   ( ( L:V List, s:Traversal, i:V. P(L,s) L:V List, s:Traversal, i:V. P(L,s)   P(L @ [i],dfs(the_obj;s;i))) P(L @ [i],dfs(the_obj;s;i)))   ( ( L:V List. P(L,dfsl(the_obj;L))) L:V List. P(L,dfsl(the_obj;L))) |
| THM | dfsl-induction2 | For any graph
 the_obj:GraphObject(the_graph), P:((V List) the_obj:GraphObject(the_graph), P:((V List)  Traversal Traversal  Prop). P(nil,nil) Prop). P(nil,nil)   ( ( L:V List, s:Traversal, i:V. paren(V;s) L:V List, s:Traversal, i:V. paren(V;s)   no_repeats(V+V;s) no_repeats(V+V;s)   P(L,s) P(L,s)   P(L @ [i],dfs(the_obj;s;i))) P(L @ [i],dfs(the_obj;s;i)))   ( ( L:V List. paren(V;dfsl(the_obj;L)) & no_repeats(V+V;dfsl(the_obj;L)) & P(L,dfsl(the_obj;L))) L:V List. paren(V;dfsl(the_obj;L)) & no_repeats(V+V;dfsl(the_obj;L)) & P(L,dfsl(the_obj;L))) |
| THM | dfsl_paren | For any graph
 the_obj:GraphObject(the_graph), L:V List. paren(V;dfsl(the_obj;L)) & no_repeats(V+V;dfsl(the_obj;L)) the_obj:GraphObject(the_graph), L:V List. paren(V;dfsl(the_obj;L)) & no_repeats(V+V;dfsl(the_obj;L)) |
| THM | dfsl_member | For any graph
 the_obj:GraphObject(the_graph), L:V List. ( the_obj:GraphObject(the_graph), L:V List. ( i i L.(inr(i) L.(inr(i)  dfsl(the_obj;L)) & (inl(i) dfsl(the_obj;L)) & (inl(i)  dfsl(the_obj;L))) dfsl(the_obj;L))) |
| THM | depthfirst-dfsl | For any graph
 the_obj:GraphObject(the_graph). the_obj:GraphObject(the_graph).  L:V List. no_repeats(V;L) & ( L:V List. no_repeats(V;L) & ( y:V. (y y:V. (y  L)) & depthfirst(the_obj) = dfsl(the_obj;L) L)) & depthfirst(the_obj) = dfsl(the_obj;L) |
| THM | depthfirst_induction | For any graph
 the_obj:GraphObject(the_graph), P:(Traversal the_obj:GraphObject(the_graph), P:(Traversal  Prop). P(nil) Prop). P(nil)   ( ( s:Traversal, i:V. P(s) s:Traversal, i:V. P(s)   P(dfs(the_obj;s;i))) P(dfs(the_obj;s;i)))   P(depthfirst(the_obj)) P(depthfirst(the_obj)) |
| THM | depthfirst_induction2 | For any graph
 the_obj:GraphObject(the_graph), P:(Traversal the_obj:GraphObject(the_graph), P:(Traversal  Prop). P(nil) Prop). P(nil)   ( ( s:Traversal, i:V. paren(V;s) s:Traversal, i:V. paren(V;s)   no_repeats(V+V;s) no_repeats(V+V;s)   P(s) P(s)   P(dfs(the_obj;s;i))) P(dfs(the_obj;s;i)))   paren(V;depthfirst(the_obj)) & no_repeats(V+V;depthfirst(the_obj)) & P(depthfirst(the_obj)) paren(V;depthfirst(the_obj)) & no_repeats(V+V;depthfirst(the_obj)) & P(depthfirst(the_obj)) |
| THM | depthfirst_paren | For any graph
 the_obj:GraphObject(the_graph). paren(V;depthfirst(the_obj)) & no_repeats(V+V;depthfirst(the_obj)) the_obj:GraphObject(the_graph). paren(V;depthfirst(the_obj)) & no_repeats(V+V;depthfirst(the_obj)) |
| THM | depthfirst_member | For any graph
 the_obj:GraphObject(the_graph), i:V. (inr(i) the_obj:GraphObject(the_graph), i:V. (inr(i)  depthfirst(the_obj)) & (inl(i) depthfirst(the_obj)) & (inl(i)  depthfirst(the_obj)) depthfirst(the_obj)) |
| THM | depthfirst-df-traversal | For any graph
 the_obj:GraphObject(the_graph). df-traversal(the_graph;depthfirst(the_obj)) the_obj:GraphObject(the_graph). df-traversal(the_graph;depthfirst(the_obj)) |
| THM | depthfirst-properties | For any graph
 the_obj:GraphObject(the_graph). paren(V;depthfirst(the_obj)) & no_repeats(V+V;depthfirst(the_obj)) & df-traversal(the_graph;depthfirst(the_obj)) & depthfirst-traversal(the_graph;depthfirst(the_obj)) & ( the_obj:GraphObject(the_graph). paren(V;depthfirst(the_obj)) & no_repeats(V+V;depthfirst(the_obj)) & df-traversal(the_graph;depthfirst(the_obj)) & depthfirst-traversal(the_graph;depthfirst(the_obj)) & ( i:V. (inr(i) i:V. (inr(i)  depthfirst(the_obj)) & (inl(i) depthfirst(the_obj)) & (inl(i)  depthfirst(the_obj))) depthfirst(the_obj))) |
| def | topsort | topsort(G) == mapoutl(depthfirst(G)) |
| THM | topsort-properties | For any graph
 the_obj:GraphObject(the_graph). (non-trivial-loop-free(the_graph) the_obj:GraphObject(the_graph). (non-trivial-loop-free(the_graph)   topsorted(the_graph;topsort(the_obj))) & ( topsorted(the_graph;topsort(the_obj))) & ( i:V. (i i:V. (i  topsort(the_obj))) & no_repeats(V;topsort(the_obj)) topsort(the_obj))) & no_repeats(V;topsort(the_obj)) |
| THM | topsort-exists | For any graph
 the_obj:GraphObject(the_graph). the_obj:GraphObject(the_graph).  L:V List. (non-trivial-loop-free(the_graph) L:V List. (non-trivial-loop-free(the_graph)   topsorted(the_graph;L)) & ( topsorted(the_graph;L)) & ( i:V. (i i:V. (i  L)) & no_repeats(V;L) L)) & no_repeats(V;L) |
| THM | dfs-dfl-traversal | For any graph
 the_obj:GraphObject(the_graph), L:V List, s:Traversal, x:V. dfl-traversal(the_graph;L;s) the_obj:GraphObject(the_graph), L:V List, s:Traversal, x:V. dfl-traversal(the_graph;L;s)   ( ( j:V. (inr(j) j:V. (inr(j)  s) s)    (inl(j) (inl(j)  s) s)   j-the_graph- > *x) j-the_graph- > *x)   dfl-traversal(the_graph;L @ [x];dfs(the_obj;s;x)) dfl-traversal(the_graph;L @ [x];dfs(the_obj;s;x)) |
| THM | dfsl-properties | For any graph
 the_obj:GraphObject(the_graph), L:V List. paren(V;dfsl(the_obj;L)) & no_repeats(V+V;dfsl(the_obj;L)) & dfsl-traversal(the_graph;L;dfsl(the_obj;L)) & ( the_obj:GraphObject(the_graph), L:V List. paren(V;dfsl(the_obj;L)) & no_repeats(V+V;dfsl(the_obj;L)) & dfsl-traversal(the_graph;L;dfsl(the_obj;L)) & ( i:V. (i i:V. (i  L) L)   (inr(i) (inr(i)  dfsl(the_obj;L)) & (inl(i) dfsl(the_obj;L)) & (inl(i)  dfsl(the_obj;L))) dfsl(the_obj;L))) |
| def | topsortl | topsortl(A;L) == mapoutl(dfsl(A;L)) |
| THM | topsortl-properties | For any graph
 the_obj:GraphObject(the_graph), L:V List. ( the_obj:GraphObject(the_graph), L:V List. ( i:V. (i i:V. (i  L)) L))   (non-trivial-loop-free(the_graph) (non-trivial-loop-free(the_graph)   topsortedl(the_graph;L;topsortl(the_obj;L))) & ( topsortedl(the_graph;L;topsortl(the_obj;L))) & ( i:V. (i i:V. (i  topsortl(the_obj;L))) & no_repeats(V;topsortl(the_obj;L)) topsortl(the_obj;L))) & no_repeats(V;topsortl(the_obj;L)) |
| def | adjmatrix | AdjMatrix == size:   size size   size size  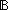 |
| def | adjm_size | t.size == 1of(t) |
| def | adjm_adj | t.adj == 2of(t) |
| def | mk_adjmatrix | mk_adjmatrix(size, adj) == < size,adj > |
| def | case_mk_adjmatrix | Case mk_adjmatrix(size,adj) = > body(size;adj)(x,z) == x/x2,x1. body(x2;x1) |
| def | adjm-graph | adjm-graph(A) == < vertices =  A.size, edges = {p:( A.size, edges = {p:( A.size A.size  A.size)| A.adj(1of(p),2of(p)) }, incidence = A.size)| A.adj(1of(p),2of(p)) }, incidence =  e.e > e.e > |
| def | eq_adjm | x =M= y == x=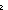 y y |
| THM | assert_eq_adjm |  M:AdjMatrix, x,y:Vertices(adjm-graph(M)). x =M= y M:AdjMatrix, x,y:Vertices(adjm-graph(M)). x =M= y   x = y x = y |
| def | adjm-vertex-accum | adjm-vertex-accum(M;s',x.f(s';x);s) == primrec(M.size;s; x,s'. f(s';x)) x,s'. f(s';x)) |
| THM | adjm-vertex-accum-properties |  M:AdjMatrix, T:Type, s:T, f:(T M:AdjMatrix, T:Type, s:T, f:(T  Vertices(adjm-graph(M)) Vertices(adjm-graph(M))  T). T).  L:Vertices(adjm-graph(M)) List. no_repeats(Vertices(adjm-graph(M));L) & ( L:Vertices(adjm-graph(M)) List. no_repeats(Vertices(adjm-graph(M));L) & ( y:Vertices(adjm-graph(M)). (y y:Vertices(adjm-graph(M)). (y  L)) & adjm-vertex-accum(M;s',x'.f(s',x');s) = list_accum(s',x'.f(s',x');s;L) L)) & adjm-vertex-accum(M;s',x'.f(s',x');s) = list_accum(s',x'.f(s',x');s;L) |
| def | adjm-edge-accum | adjm-edge-accum(M;s',x'.f(s';x');s;x) == primrec(M.size;s; y,s'. if M.adj(x,y) y,s'. if M.adj(x,y)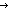 f(s';y) else s' fi) f(s';y) else s' fi) |
| THM | adjm-edge-accum-properties |  M:AdjMatrix, T:Type, s:T, x:Vertices(adjm-graph(M)), f:(T M:AdjMatrix, T:Type, s:T, x:Vertices(adjm-graph(M)), f:(T  Vertices(adjm-graph(M)) Vertices(adjm-graph(M))  T). T).  L:Vertices(adjm-graph(M)) List. ( L:Vertices(adjm-graph(M)) List. ( y:Vertices(adjm-graph(M)). x-adjm-graph(M)- > y y:Vertices(adjm-graph(M)). x-adjm-graph(M)- > y   (y (y  L)) & adjm-edge-accum(M;s',x'.f(s',x');s;x) = list_accum(s',x'.f(s',x');s;L) L)) & adjm-edge-accum(M;s',x'.f(s',x');s;x) = list_accum(s',x'.f(s',x');s;L) |
| def | adjm-obj | adjm-obj{\\\\v:l,i:l}(M) == mkgraphobj( x,y. x =M= y, ext{assert_eq_adjm}(M), x,y. x =M= y, ext{assert_eq_adjm}(M),  f,s,x. adjm-edge-accum(M;s',x'.f(s',x');s;x), ext{adjm_DASH_edge_DASH_accum_DASH_properties}{i:l}(M), f,s,x. adjm-edge-accum(M;s',x'.f(s',x');s;x), ext{adjm_DASH_edge_DASH_accum_DASH_properties}{i:l}(M),  f,s. adjm-vertex-accum(M;s',x'.f(s',x');s), ext{adjm_DASH_vertex_DASH_accum_DASH_properties}{i:l}(M), f,s. adjm-vertex-accum(M;s',x'.f(s',x');s), ext{adjm_DASH_vertex_DASH_accum_DASH_properties}{i:l}(M), 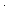 ) ) |
| def | adjm-rep | adjm-rep{\\\\v:l,i:l}() == mkgraphrep(AdjMatrix,  M.adjm-graph(M), M.adjm-graph(M),  M.adjm-obj{\\\\v:l,i:l}(M)) M.adjm-obj{\\\\v:l,i:l}(M)) |
| def | adjlist | AdjList == size:   size size  ( ( size List) size List) |
| def | adjl_size | t.size == 1of(t) |
| def | adjl_out | t.out == 2of(t) |
| def | mk_adjlist | mk_adjlist(size, out) == < size,out > |
| def | case_mk_adjlist | Case mk_adjlist(size; out ) = > body(size;out)(x,z) == x/x2,x1. body(x2;x1) |
| def | adjl-graph | adjl-graph(G) == < vertices =  G.size, edges = x: G.size, edges = x: G.size G.size  ||G.out(x)||, incidence = ||G.out(x)||, incidence =  e. < 1of(e),(G.out(1of(e)))[2of(e)] > > e. < 1of(e),(G.out(1of(e)))[2of(e)] > > |
| def | eq_adjl | x =A= y == x=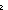 y y |
| THM | assert_eq_adjl |  A:AdjList, x,y:Vertices(adjl-graph(A)). x =A= y A:AdjList, x,y:Vertices(adjl-graph(A)). x =A= y   x = y x = y |
| def | adjl-edge-accum | adjl-edge-accum(A;s',x'.f(s';x');s;x) == list_accum(s',x'.f(s';x');s;A.out(x)) |
| THM | adjl-edge-accum-properties |  A:AdjList, T:Type, s:T, x:Vertices(adjl-graph(A)), f:(T A:AdjList, T:Type, s:T, x:Vertices(adjl-graph(A)), f:(T  Vertices(adjl-graph(A)) Vertices(adjl-graph(A))  T). T).  L:Vertices(adjl-graph(A)) List. ( L:Vertices(adjl-graph(A)) List. ( y:Vertices(adjl-graph(A)). x-adjl-graph(A)- > y y:Vertices(adjl-graph(A)). x-adjl-graph(A)- > y   (y (y  L)) & adjl-edge-accum(A;s',x'.f(s',x');s;x) = list_accum(s',x'.f(s',x');s;L) L)) & adjl-edge-accum(A;s',x'.f(s',x');s;x) = list_accum(s',x'.f(s',x');s;L) |
| def | adjl-vertex-accum | adjl-vertex-accum(A;s',x.f(s';x);s) == primrec(A.size;s; x,s'. f(s';x)) x,s'. f(s';x)) |
| THM | adjl-vertex-accum-properties |  A:AdjList, T:Type, s:T, f:(T A:AdjList, T:Type, s:T, f:(T  Vertices(adjl-graph(A)) Vertices(adjl-graph(A))  T). T).  L:Vertices(adjl-graph(A)) List. no_repeats(Vertices(adjl-graph(A));L) & ( L:Vertices(adjl-graph(A)) List. no_repeats(Vertices(adjl-graph(A));L) & ( y:Vertices(adjl-graph(A)). (y y:Vertices(adjl-graph(A)). (y  L)) & adjl-vertex-accum(A;s',x'.f(s',x');s) = list_accum(s',x'.f(s',x');s;L) L)) & adjl-vertex-accum(A;s',x'.f(s',x');s) = list_accum(s',x'.f(s',x');s;L) |
| def | adjl-obj | adjl-obj{\\\\v:l,i:l}(A) == mkgraphobj( x,y. x =A= y, ext{assert_eq_adjl}(A), x,y. x =A= y, ext{assert_eq_adjl}(A),  f,s,x. adjl-edge-accum(A;s',x'.f(s',x');s;x), ext{adjl_DASH_edge_DASH_accum_DASH_properties}{i:l}(A), f,s,x. adjl-edge-accum(A;s',x'.f(s',x');s;x), ext{adjl_DASH_edge_DASH_accum_DASH_properties}{i:l}(A),  f,s. adjl-vertex-accum(A;s',x'.f(s',x');s), ext{adjl_DASH_vertex_DASH_accum_DASH_properties}{i:l}(A), f,s. adjl-vertex-accum(A;s',x'.f(s',x');s), ext{adjl_DASH_vertex_DASH_accum_DASH_properties}{i:l}(A), 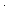 ) ) |
| def | adjl-rep | AdjListRep == mkgraphrep(AdjList,  A.adjl-graph(A), A.adjl-graph(A),  A.adjl-obj{\\\\v:l,i:l}(A)) A.adjl-obj{\\\\v:l,i:l}(A)) |
| def | adjm_to_adjl | adjm_to_adjl(m) == Case(m) Case mk_adjmatrix(n,f) = > mk_adjlist(n,  i.filter( i.filter( j.f(i,j);upto(0;n))) j.f(i,j);upto(0;n))) |
| THM | adjm_to_adjl_graph |  m:AdjMatrix. adjl-graph(adjm_to_adjl(m)) m:AdjMatrix. adjl-graph(adjm_to_adjl(m))  adjm-graph(m) adjm-graph(m) |
| def | adjl_to_adjm | adjl_to_adjm(l) == Case(l) Case mk_adjlist(n; out ) = > mk_adjmatrix(n,  i,j. ( i,j. ( k k out(i).k= out(i).k=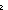 j)) j)) |