Thm*  b: b: . . 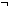 b b 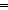  b = false b = false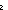 | [not_assert_imp_eq_bfalse] |
Thm*  b: b: . b . b 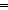  b = true b = true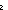 | [assert_imp_eq_btrue] |
Thm*  P:(('a P:(('a  'a 'a   ) )  Prop). Prop).
Thm* P(<eq_pred:(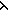 x:'a. x:'a. 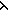 y:'a. x = y:'a. x = y)>) y)>) 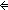  ( ( f:eq('a). P(f)) f:eq('a). P(f)) | [eq_pred_abstraction] |
Thm*  f:eq('a). f = ( f:eq('a). f = (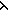 x:'a. x:'a. 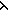 y:'a. x = y:'a. x = y) y)  'a 'a  'a 'a   | [eq_pred_char] |
Thm* eq('a) 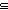 ('a ('a  'a 'a   ) ) | [eq_pred_inc] |
Thm*  'a,'b:S. 'a,'b:S.
Thm* (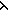 p:'a p:'a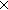 'b. 'b. 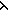 a:'a. a:'a. 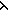 b:'b. (a = b:'b. (a = 1of(p)) 1of(p))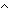 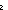 (b = (b = 2of(p))) 2of(p)))
Thm* =
Thm* (@ rep:'a rep:'a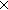 'b 'b  'a 'a  'b 'b  
Thm* (@ (( ((  p',p'':'a p',p'':'a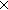 'b. ((rep(p')) = 'b. ((rep(p')) = (rep(p''))) (rep(p'')))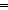  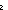 (p' = (p' = p'')) p''))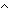 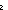
Thm* (@ ( (  x:'a x:'a  'b 'b  
Thm* (@ ( (  ((his_pair('a; 'b)(x)) = ((his_pair('a; 'b)(x)) = ( (  p':'a p':'a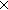 'b. (x = 'b. (x = (rep(p')))))))) (rep(p')))))))) | [rep_prod_axiom] |
Thm*  'a,'b:S, P:('b 'a,'b:S, P:('b   ), rep:('a ), rep:('a  'b), abs:('b 'b), abs:('b  'a), a:'a, r:'b. 'a), a:'a, r:'b.
Thm* iso_pair('a;'b;P;rep;abs) 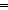  rep(a) = r rep(a) = r 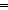  a = abs(r) a = abs(r) | [iso_pair_rep_to_abs] |
Thm*  'a,'b:S, P:('b 'a,'b:S, P:('b   ), rep:('a ), rep:('a  'b), abs:('b 'b), abs:('b  'a). 'a).
Thm* iso_pair('a;'b;P;rep;abs)
Thm* 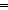 
Thm* ( a:'a. abs(rep(a)) = a) & ( a:'a. abs(rep(a)) = a) & ( r:'b. P(r) = ((rep(abs(r))) = r:'b. P(r) = ((rep(abs(r))) = r)) r)) | [iso_pair_char] |
Thm*  p: p: . . 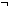 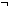 p p 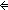  p p | [not_not] |
Thm*  p,q: p,q: . . 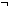 (p (p 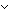 q) q) 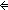  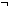 p & p & 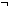 q q | [not_or] |
Thm*  p,q: p,q: . . 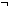 (p & q) (p & q) 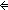  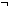 p p 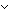 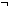 q q | [not_and] |
Thm*  T:S, P:(T T:S, P:(T   ). ). 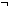 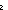 ( (  x:T. P(x)) = ( x:T. P(x)) = (  x:T. x:T. 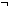 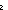 P(x)) P(x)) | [bnot_ball] |
Thm*  T:S, P:(T T:S, P:(T   ). ). 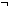 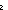 ( (  x:T. P(x)) = ( x:T. P(x)) = (  x:T. x:T. 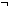 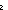 P(x)) P(x)) | [bnot_bexists] |
Thm*  'a,'b:S, P:('b 'a,'b:S, P:('b   ), rep:('a ), rep:('a  'b), abs:('b 'b), abs:('b  'a). 'a).
Thm* iso_pair('a;'b;P;rep;abs)
Thm* 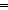 
Thm* ( rep':('a rep':('a  'b). type_definition('b;'a;P;rep')) 'b). type_definition('b;'a;P;rep')) | [type_def_iso] |
Thm*  'a,'b:S, P:('b 'a,'b:S, P:('b   ), rep:('a ), rep:('a  'b), abs:('b 'b), abs:('b  'a). 'a).
Thm* iso_pair('a;'b;P;rep;abs)  Prop Prop | [iso_pair_wf] |
Thm*  A,B:Type, x:A+B. isr(x) A,B:Type, x:A+B. isr(x)   | [isr_wf] |
Thm*  A:Type, b: A:Type, b: , x:(b , x:(b  A), y:(( A), y:((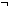 b) b)  A). bif(b; bx.x(bx); by.y(by)) A). bif(b; bx.x(bx); by.y(by))  A A | [bif_wf] |
Thm*  x,y: x,y: . (x = . (x = y) y) 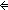  (x (x 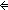  y) y) | [assert_of_bequal_bools] |
Thm*  x,y: x,y: . x = y . x = y 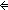  (x (x 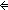  y) y) | [bequal_bools] |
Thm* false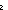 = true = true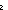 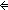  False False | [btrue_neq_bfalse_simp_2] |
Thm* true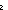 = false = false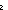 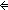  False False | [btrue_neq_bfalse_simp_1] |
Thm*  T:Type, x,y:T. (x = T:Type, x,y:T. (x = y) y)   | [bequal_wf] |
Thm*  P:(T P:(T   ). ( ). (  x:T. P(x)) x:T. P(x)) 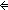  ( ( x:T. P(x)) x:T. P(x)) | [assert_of_bexists] |
Thm*  T:Type, P:(T T:Type, P:(T   ). ( ). (  x:T. P(x)) x:T. P(x))   | [bexists_wf] |
Thm*  P:(T P:(T   ). ( ). (  x:T. P(x)) x:T. P(x)) 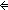  ( ( x:T. P(x)) x:T. P(x)) | [assert_of_ball] |
Thm*  T:Type, P:(T T:Type, P:(T   ). ( ). (  x:T. P(x)) x:T. P(x))   | [ball_wf] |
Thm*  P: P: . ( . (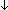  P) = P P) = P | [prop_to_bool_char_2] |
Thm*  P:Prop{2}. ( P:Prop{2}. (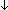  P) P)   | [prop_to_bool_2_wf] |
Def eq('a) == {f:('a  'a 'a   )| f = ( )| f = (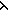 x:'a. x:'a. 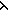 y:'a. x = y:'a. x = y) } y) } | [eq_pred] |