Thm* all
Thm* ( k:hnum. all k:hnum. all
Thm* ( k:hnum. ( k:hnum. ( n:hnum. implies n:hnum. implies
Thm* ( k:hnum. ( k:hnum. ( n:hnum. (lt(0,n) n:hnum. (lt(0,n)
Thm* ( k:hnum. ( k:hnum. ( n:hnum. ,exists n:hnum. ,exists
Thm* ( k:hnum. ( k:hnum. ( n:hnum. ,( n:hnum. ,( r:hnum. exists r:hnum. exists
Thm* ( k:hnum. ( k:hnum. ( n:hnum. ,( n:hnum. ,( r:hnum. ( r:hnum. ( q:hnum. and q:hnum. and
Thm* ( k:hnum. ( k:hnum. ( n:hnum. ,( n:hnum. ,( r:hnum. ( r:hnum. ( q:hnum. (equal(k,add(mult(q,n),r)) q:hnum. (equal(k,add(mult(q,n),r))
Thm* ( k:hnum. ( k:hnum. ( n:hnum. ,( n:hnum. ,( r:hnum. ( r:hnum. ( q:hnum. ,lt(r,n))))))) q:hnum. ,lt(r,n))))))) | [hda] |
Thm* all
Thm* ( P:hnum P:hnum  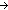 hbool. implies hbool. implies
Thm* ( P:hnum P:hnum   hbool. (exists( hbool. (exists( n:hnum. P(n)) n:hnum. P(n))
Thm* ( P:hnum P:hnum   hbool. ,exists hbool. ,exists
Thm* ( P:hnum P:hnum   hbool. ,( hbool. ,( n:hnum. and n:hnum. and
Thm* ( P:hnum P:hnum   hbool. ,( hbool. ,( n:hnum. (P(n) n:hnum. (P(n)
Thm* ( P:hnum P:hnum   hbool. ,( hbool. ,( n:hnum. ,all( n:hnum. ,all( m:hnum. implies(lt(m,n),not(P(m)))))))) m:hnum. implies(lt(m,n),not(P(m)))))))) | [hwop] |
Thm* all( n:hnum. all( n:hnum. all( m:hnum. or(lt(n,m),exists( m:hnum. or(lt(n,m),exists( p:hnum. equal(n,add(p,m)))))) p:hnum. equal(n,add(p,m)))))) | [hless_or_eq_add] |
Thm* all
Thm* ( m:hnum. all m:hnum. all
Thm* ( m:hnum. ( m:hnum. ( n:hnum. implies n:hnum. implies
Thm* ( m:hnum. ( m:hnum. ( n:hnum. (lt(n,m) n:hnum. (lt(n,m)
Thm* ( m:hnum. ( m:hnum. ( n:hnum. ,exists( n:hnum. ,exists( p:hnum. equal(m,add(n,add(p,1))))))) p:hnum. equal(m,add(n,add(p,1))))))) | [hless_add_1] |
Thm* all
Thm* ( m:hnum. all m:hnum. all
Thm* ( m:hnum. ( m:hnum. ( n:hnum. implies(lt(n,m),exists( n:hnum. implies(lt(n,m),exists( p:hnum. equal(add(p,n),m))))) p:hnum. equal(add(p,n),m))))) | [hless_add] |
Thm* all( m:hnum. or(equal(m,0),exists( m:hnum. or(equal(m,0),exists( n:hnum. equal(m,suc(n))))) n:hnum. equal(m,suc(n))))) | [hnum_cases] |