Selected Objects
| THM | hndiv_unique |
all
( n:hnum. all n:hnum. all
( n:hnum. ( n:hnum. ( k:hnum. all k:hnum. all
( n:hnum. ( n:hnum. ( k:hnum. ( k:hnum. ( q:hnum. implies q:hnum. implies
( n:hnum. ( n:hnum. ( k:hnum. ( k:hnum. ( q:hnum. (exists q:hnum. (exists
( n:hnum. ( n:hnum. ( k:hnum. ( k:hnum. ( q:hnum. (( q:hnum. (( r:hnum. and(equal(k,add(mult(q,n),r)),lt(r,n))) r:hnum. and(equal(k,add(mult(q,n),r)),lt(r,n)))
( n:hnum. ( n:hnum. ( k:hnum. ( k:hnum. ( q:hnum. ,equal(div(k,n),q))))) q:hnum. ,equal(div(k,n),q))))) |
| THM | hmod_unique |
all
( n:hnum. all n:hnum. all
( n:hnum. ( n:hnum. ( k:hnum. all k:hnum. all
( n:hnum. ( n:hnum. ( k:hnum. ( k:hnum. ( r:hnum. implies r:hnum. implies
( n:hnum. ( n:hnum. ( k:hnum. ( k:hnum. ( r:hnum. (exists r:hnum. (exists
( n:hnum. ( n:hnum. ( k:hnum. ( k:hnum. ( r:hnum. (( r:hnum. (( q:hnum. and(equal(k,add(mult(q,n),r)),lt(r,n))) q:hnum. and(equal(k,add(mult(q,n),r)),lt(r,n)))
( n:hnum. ( n:hnum. ( k:hnum. ( k:hnum. ( r:hnum. ,equal(mod(k,n),r))))) r:hnum. ,equal(mod(k,n),r))))) |
| THM | hdiv_mult |
all
( n:hnum. all n:hnum. all
( n:hnum. ( n:hnum. ( r:hnum. implies r:hnum. implies
( n:hnum. ( n:hnum. ( r:hnum. (lt(r,n) r:hnum. (lt(r,n)
( n:hnum. ( n:hnum. ( r:hnum. ,all( r:hnum. ,all( q:hnum. equal(div(add(mult(q,n),r),n),q))))) q:hnum. equal(div(add(mult(q,n),r),n),q))))) |
| THM | hless_mod |
all( n:hnum. all( n:hnum. all( k:hnum. implies(lt(k,n),equal(mod(k,n),k)))) k:hnum. implies(lt(k,n),equal(mod(k,n),k)))) |
| THM | hmod_eq_0 |
all( n:hnum. implies(lt(0,n),all( n:hnum. implies(lt(0,n),all( k:hnum. equal(mod(mult(k,n),n),0)))) k:hnum. equal(mod(mult(k,n),n),0)))) |
| THM | hzero_mod |
all( n:hnum. implies(lt(0,n),equal(mod(0,n),0))) n:hnum. implies(lt(0,n),equal(mod(0,n),0))) |
| THM | hzero_div |
all( n:hnum. implies(lt(0,n),equal(div(0,n),0))) n:hnum. implies(lt(0,n),equal(div(0,n),0))) |
| THM | hmod_mult |
all
( n:hnum. all n:hnum. all
( n:hnum. ( n:hnum. ( r:hnum. implies r:hnum. implies
( n:hnum. ( n:hnum. ( r:hnum. (lt(r,n) r:hnum. (lt(r,n)
( n:hnum. ( n:hnum. ( r:hnum. ,all( r:hnum. ,all( q:hnum. equal(mod(add(mult(q,n),r),n),r))))) q:hnum. equal(mod(add(mult(q,n),r),n),r))))) |
| THM | hmod_times |
all
( n:hnum. implies n:hnum. implies
( n:hnum. (lt(0,n) n:hnum. (lt(0,n)
( n:hnum. ,all( n:hnum. ,all( q:hnum. all( q:hnum. all( r:hnum. equal(mod(add(mult(q,n),r),n),mod(r,n)))))) r:hnum. equal(mod(add(mult(q,n),r),n),mod(r,n)))))) |
| THM | hmod_plus |
all
( n:hnum. implies n:hnum. implies
( n:hnum. (lt(0,n) n:hnum. (lt(0,n)
( n:hnum. ,all n:hnum. ,all
( n:hnum. ,( n:hnum. ,( j:hnum. all j:hnum. all
( n:hnum. ,( n:hnum. ,( j:hnum. ( j:hnum. ( k:hnum. equal k:hnum. equal
( n:hnum. ,( n:hnum. ,( j:hnum. ( j:hnum. ( k:hnum. (mod(add(mod(j,n),mod(k,n)),n) k:hnum. (mod(add(mod(j,n),mod(k,n)),n)
( n:hnum. ,( n:hnum. ,( j:hnum. ( j:hnum. ( k:hnum. ,mod(add(j,k),n)))))) k:hnum. ,mod(add(j,k),n)))))) |
| THM | hmod_mod |
all( n:hnum. implies(lt(0,n),all( n:hnum. implies(lt(0,n),all( k:hnum. equal(mod(mod(k,n),n),mod(k,n))))) k:hnum. equal(mod(mod(k,n),n),mod(k,n))))) |
| THM | hsub_mono_eq |
all( n:hnum. all( n:hnum. all( m:hnum. equal(sub(suc(n),suc(m)),sub(n,m)))) m:hnum. equal(sub(suc(n),suc(m)),sub(n,m)))) |
| THM | hsub_plus |
all( a:hnum. all( a:hnum. all( b:hnum. all( b:hnum. all( c:hnum. equal(sub(a,add(b,c)),sub(sub(a,b),c))))) c:hnum. equal(sub(a,add(b,c)),sub(sub(a,b),c))))) |
| THM | hinv_pre_less |
all( m:hnum. implies(lt(0,m),all( m:hnum. implies(lt(0,m),all( n:hnum. equal(lt(pre(m),pre(n)),lt(m,n))))) n:hnum. equal(lt(pre(m),pre(n)),lt(m,n))))) |
| THM | hinv_pre_less_eq |
all( n:hnum. implies(lt(0,n),all( n:hnum. implies(lt(0,n),all( m:hnum. equal(le(pre(m),pre(n)),le(m,n))))) m:hnum. equal(le(pre(m),pre(n)),le(m,n))))) |
| THM | hsub_less_eq |
all( n:hnum. all( n:hnum. all( m:hnum. le(sub(n,m),n))) m:hnum. le(sub(n,m),n))) |
| THM | hsub_eq_eq_0 |
all( m:hnum. all( m:hnum. all( n:hnum. equal(equal(sub(m,n),m),or(equal(m,0),equal(n,0))))) n:hnum. equal(equal(sub(m,n),m),or(equal(m,0),equal(n,0))))) |
| THM | hsub_less_0 |
all( n:hnum. all( n:hnum. all( m:hnum. equal(lt(m,n),lt(0,sub(n,m))))) m:hnum. equal(lt(m,n),lt(0,sub(n,m))))) |
| THM | hsub_less_or |
all( m:hnum. all( m:hnum. all( n:hnum. implies(lt(n,m),le(n,sub(m,1))))) n:hnum. implies(lt(n,m),le(n,sub(m,1))))) |
| THM | hless_sub_add_less |
all( n:hnum. all( n:hnum. all( m:hnum. all( m:hnum. all( i:hnum. implies(lt(i,sub(n,m)),lt(add(i,m),n))))) i:hnum. implies(lt(i,sub(n,m)),lt(add(i,m),n))))) |
| THM | htimes2 |
all( n:hnum. equal(mult(2,n),add(n,n))) n:hnum. equal(mult(2,n),add(n,n))) |
| THM | hless_mult_mono |
all
( m:hnum. all m:hnum. all
( m:hnum. ( m:hnum. ( i:hnum. all i:hnum. all
( m:hnum. ( m:hnum. ( i:hnum. ( i:hnum. ( n:hnum. equal n:hnum. equal
( m:hnum. ( m:hnum. ( i:hnum. ( i:hnum. ( n:hnum. (lt(mult(suc(n),m),mult(suc(n),i)) n:hnum. (lt(mult(suc(n),m),mult(suc(n),i))
( m:hnum. ( m:hnum. ( i:hnum. ( i:hnum. ( n:hnum. ,lt(m,i))))) n:hnum. ,lt(m,i))))) |
| THM | hmult_mono_eq |
all
( m:hnum. all m:hnum. all
( m:hnum. ( m:hnum. ( i:hnum. all i:hnum. all
( m:hnum. ( m:hnum. ( i:hnum. ( i:hnum. ( n:hnum. equal n:hnum. equal
( m:hnum. ( m:hnum. ( i:hnum. ( i:hnum. ( n:hnum. (equal(mult(suc(n),m),mult(suc(n),i)) n:hnum. (equal(mult(suc(n),m),mult(suc(n),i))
( m:hnum. ( m:hnum. ( i:hnum. ( i:hnum. ( n:hnum. ,equal(m,i))))) n:hnum. ,equal(m,i))))) |
| THM | hadd_sub |
all( a:hnum. all( a:hnum. all( c:hnum. equal(sub(add(a,c),c),a))) c:hnum. equal(sub(add(a,c),c),a))) |
| THM | hless_eq_add_sub |
all
( c:hnum. all c:hnum. all
( c:hnum. ( c:hnum. ( b:hnum. implies b:hnum. implies
( c:hnum. ( c:hnum. ( b:hnum. (le(c,b) b:hnum. (le(c,b)
( c:hnum. ( c:hnum. ( b:hnum. ,all( b:hnum. ,all( a:hnum. equal(sub(add(a,b),c),add(a,sub(b,c))))))) a:hnum. equal(sub(add(a,b),c),add(a,sub(b,c))))))) |
| THM | hsub_equal_0 |
all( c:hnum. equal(sub(c,c),0)) c:hnum. equal(sub(c,c),0)) |
| THM | hless_eq_sub_less |
all
( a:hnum. all a:hnum. all
( a:hnum. ( a:hnum. ( b:hnum. implies b:hnum. implies
( a:hnum. ( a:hnum. ( b:hnum. (le(b,a) b:hnum. (le(b,a)
( a:hnum. ( a:hnum. ( b:hnum. ,all( b:hnum. ,all( c:hnum. equal(lt(sub(a,b),c),lt(a,add(b,c))))))) c:hnum. equal(lt(sub(a,b),c),lt(a,add(b,c))))))) |
| THM | hnot_suc_less_eq |
all( n:hnum. all( n:hnum. all( m:hnum. equal(not(le(suc(n),m)),le(m,n)))) m:hnum. equal(not(le(suc(n),m)),le(m,n)))) |
| THM | hsub_sub |
all
( b:hnum. all b:hnum. all
( b:hnum. ( b:hnum. ( c:hnum. implies c:hnum. implies
( b:hnum. ( b:hnum. ( c:hnum. (le(c,b) c:hnum. (le(c,b)
( b:hnum. ( b:hnum. ( c:hnum. ,all( c:hnum. ,all( a:hnum. equal(sub(a,sub(b,c)),sub(add(a,c),b)))))) a:hnum. equal(sub(a,sub(b,c)),sub(add(a,c),b)))))) |
| THM | hless_imp_less_add |
all( n:hnum. all( n:hnum. all( m:hnum. implies(lt(n,m),all( m:hnum. implies(lt(n,m),all( p:hnum. lt(n,add(m,p)))))) p:hnum. lt(n,add(m,p)))))) |
| THM | hless_eq_imp_less_suc |
all( n:hnum. all( n:hnum. all( m:hnum. implies(le(n,m),lt(n,suc(m))))) m:hnum. implies(le(n,m),lt(n,suc(m))))) |
| THM | hsub_less_eq_add |
all
( m:hnum. all m:hnum. all
( m:hnum. ( m:hnum. ( p:hnum. implies p:hnum. implies
( m:hnum. ( m:hnum. ( p:hnum. (le(m,p) p:hnum. (le(m,p)
( m:hnum. ( m:hnum. ( p:hnum. ,all( p:hnum. ,all( n:hnum. equal(le(sub(p,m),n),le(p,add(m,n))))))) n:hnum. equal(le(sub(p,m),n),le(p,add(m,n))))))) |
| THM | hsub_cancel |
all
( p:hnum. all p:hnum. all
( p:hnum. ( p:hnum. ( n:hnum. all n:hnum. all
( p:hnum. ( p:hnum. ( n:hnum. ( n:hnum. ( m:hnum. implies m:hnum. implies
( p:hnum. ( p:hnum. ( n:hnum. ( n:hnum. ( m:hnum. (and(le(n,p),le(m,p)) m:hnum. (and(le(n,p),le(m,p))
( p:hnum. ( p:hnum. ( n:hnum. ( n:hnum. ( m:hnum. ,equal(equal(sub(p,n),sub(p,m)),equal(n,m)))))) m:hnum. ,equal(equal(sub(p,n),sub(p,m)),equal(n,m)))))) |
| THM | hcancel_sub |
all
( p:hnum. all p:hnum. all
( p:hnum. ( p:hnum. ( n:hnum. all n:hnum. all
( p:hnum. ( p:hnum. ( n:hnum. ( n:hnum. ( m:hnum. implies m:hnum. implies
( p:hnum. ( p:hnum. ( n:hnum. ( n:hnum. ( m:hnum. (and(le(p,n),le(p,m)) m:hnum. (and(le(p,n),le(p,m))
( p:hnum. ( p:hnum. ( n:hnum. ( n:hnum. ( m:hnum. ,equal(equal(sub(n,p),sub(m,p)),equal(n,m)))))) m:hnum. ,equal(equal(sub(n,p),sub(m,p)),equal(n,m)))))) |
| THM | hnot_exp_0 |
all( m:hnum. all( m:hnum. all( n:hnum. not(equal(exp(suc(n),m),0)))) n:hnum. not(equal(exp(suc(n),m),0)))) |
| THM | hzero_less_exp |
all( m:hnum. all( m:hnum. all( n:hnum. lt(0,exp(suc(n),m)))) n:hnum. lt(0,exp(suc(n),m)))) |
| THM | hodd_or_even |
all
( n:hnum. exists n:hnum. exists
( n:hnum. ( n:hnum. ( m:hnum. or m:hnum. or
( n:hnum. ( n:hnum. ( m:hnum. (equal(n,mult(suc(suc(0)),m)) m:hnum. (equal(n,mult(suc(suc(0)),m))
( n:hnum. ( n:hnum. ( m:hnum. ,equal(n,add(mult(suc(suc(0)),m),1))))) m:hnum. ,equal(n,add(mult(suc(suc(0)),m),1))))) |
| THM | hless_exp_suc_mono |
all( n:hnum. all( n:hnum. all( m:hnum. lt(exp(suc(suc(m)),n),exp(suc(suc(m)),suc(n))))) m:hnum. lt(exp(suc(suc(m)),n),exp(suc(suc(m)),suc(n))))) |
| THM | hless_less_cases |
all( m:hnum. all( m:hnum. all( n:hnum. or(equal(m,n),or(lt(m,n),lt(n,m))))) n:hnum. or(equal(m,n),or(lt(m,n),lt(n,m))))) |
| THM | hgreater_eq |
all( n:hnum. all( n:hnum. all( m:hnum. equal(ge(n,m),le(m,n)))) m:hnum. equal(ge(n,m),le(m,n)))) |
| THM | hless_eq_cases |
all( m:hnum. all( m:hnum. all( n:hnum. or(le(m,n),le(n,m)))) n:hnum. or(le(m,n),le(n,m)))) |
| THM | hless_equal_add |
all( m:hnum. all( m:hnum. all( n:hnum. implies(le(m,n),exists( n:hnum. implies(le(m,n),exists( p:hnum. equal(n,add(m,p)))))) p:hnum. equal(n,add(m,p)))))) |
| THM | hless_eq_exists |
all( m:hnum. all( m:hnum. all( n:hnum. equal(le(m,n),exists( n:hnum. equal(le(m,n),exists( p:hnum. equal(n,add(m,p)))))) p:hnum. equal(n,add(m,p)))))) |
| THM | hnot_less_equal |
all( m:hnum. all( m:hnum. all( n:hnum. equal(not(le(m,n)),lt(n,m)))) n:hnum. equal(not(le(m,n)),lt(n,m)))) |
| THM | hless_eq_0 |
all( n:hnum. equal(le(n,0),equal(n,0))) n:hnum. equal(le(n,0),equal(n,0))) |
| THM | hmult_eq_0 |
all( m:hnum. all( m:hnum. all( n:hnum. equal(equal(mult(m,n),0),or(equal(m,0),equal(n,0))))) n:hnum. equal(equal(mult(m,n),0),or(equal(m,0),equal(n,0))))) |
| THM | hless_mult2 |
all( m:hnum. all( m:hnum. all( n:hnum. implies(and(lt(0,m),lt(0,n)),lt(0,mult(m,n))))) n:hnum. implies(and(lt(0,m),lt(0,n)),lt(0,mult(m,n))))) |
| THM | hless_eq_less_trans |
all( m:hnum. all( m:hnum. all( n:hnum. all( n:hnum. all( p:hnum. implies(and(le(m,n),lt(n,p)),lt(m,p))))) p:hnum. implies(and(le(m,n),lt(n,p)),lt(m,p))))) |
| THM | hless_less_eq_trans |
all( m:hnum. all( m:hnum. all( n:hnum. all( n:hnum. all( p:hnum. implies(and(lt(m,n),le(n,p)),lt(m,p))))) p:hnum. implies(and(lt(m,n),le(n,p)),lt(m,p))))) |
| THM | hfact_less |
all( n:hnum. lt(0,fact(n))) n:hnum. lt(0,fact(n))) |
| THM | heven_odd |
all( n:hnum. equal(even(n),not(odd(n)))) n:hnum. equal(even(n),not(odd(n)))) |
| THM | hodd_even |
all( n:hnum. equal(odd(n),not(even(n)))) n:hnum. equal(odd(n),not(even(n)))) |
| THM | heven_or_odd |
all( n:hnum. or(even(n),odd(n))) n:hnum. or(even(n),odd(n))) |
| THM | heven_and_odd |
all( n:hnum. not(and(even(n),odd(n)))) n:hnum. not(and(even(n),odd(n)))) |
| THM | heven_add |
all( m:hnum. all( m:hnum. all( n:hnum. equal(even(add(m,n)),equal(even(m),even(n))))) n:hnum. equal(even(add(m,n)),equal(even(m),even(n))))) |
| THM | heven_mult |
all( m:hnum. all( m:hnum. all( n:hnum. equal(even(mult(m,n)),or(even(m),even(n))))) n:hnum. equal(even(mult(m,n)),or(even(m),even(n))))) |
| THM | hodd_add |
all( m:hnum. all( m:hnum. all( n:hnum. equal(odd(add(m,n)),not(equal(odd(m),odd(n)))))) n:hnum. equal(odd(add(m,n)),not(equal(odd(m),odd(n)))))) |
| THM | hodd_mult |
all( m:hnum. all( m:hnum. all( n:hnum. equal(odd(mult(m,n)),and(odd(m),odd(n))))) n:hnum. equal(odd(mult(m,n)),and(odd(m),odd(n))))) |
| THM | heven_double |
all( n:hnum. even(mult(2,n))) n:hnum. even(mult(2,n))) |
| THM | hodd_double |
all( n:hnum. odd(suc(mult(2,n)))) n:hnum. odd(suc(mult(2,n)))) |
| THM | heven_odd_exists |
all
( n:hnum. and n:hnum. and
( n:hnum. (implies(even(n),exists( n:hnum. (implies(even(n),exists( m:hnum. equal(n,mult(2,m)))) m:hnum. equal(n,mult(2,m))))
( n:hnum. ,implies(odd(n),exists( n:hnum. ,implies(odd(n),exists( m:hnum. equal(n,suc(mult(2,m))))))) m:hnum. equal(n,suc(mult(2,m))))))) |
| THM | heven_exists |
all( n:hnum. equal(even(n),exists( n:hnum. equal(even(n),exists( m:hnum. equal(n,mult(2,m))))) m:hnum. equal(n,mult(2,m))))) |
| THM | hodd_exists |
all( n:hnum. equal(odd(n),exists( n:hnum. equal(odd(n),exists( m:hnum. equal(n,suc(mult(2,m)))))) m:hnum. equal(n,suc(mult(2,m)))))) |
| THM | heq_less_eq |
all( m:hnum. all( m:hnum. all( n:hnum. equal(equal(m,n),and(le(m,n),le(n,m))))) n:hnum. equal(equal(m,n),and(le(m,n),le(n,m))))) |
| THM | hadd_mono_less_eq |
all( m:hnum. all( m:hnum. all( n:hnum. all( n:hnum. all( p:hnum. equal(le(add(m,n),add(m,p)),le(n,p))))) p:hnum. equal(le(add(m,n),add(m,p)),le(n,p))))) |
| THM | hnot_suc_less_eq_0 |
all( n:hnum. not(le(suc(n),0))) n:hnum. not(le(suc(n),0))) |
| THM | hnot_leq |
all( m:hnum. all( m:hnum. all( n:hnum. equal(not(le(m,n)),le(suc(n),m)))) n:hnum. equal(not(le(m,n)),le(suc(n),m)))) |
| THM | hnot_num_eq |
all( m:hnum. all( m:hnum. all( n:hnum. equal(not(equal(m,n)),or(le(suc(m),n),le(suc(n),m))))) n:hnum. equal(not(equal(m,n)),or(le(suc(m),n),le(suc(n),m))))) |
| THM | hnot_greater |
all( m:hnum. all( m:hnum. all( n:hnum. equal(not(gt(m,n)),le(m,n)))) n:hnum. equal(not(gt(m,n)),le(m,n)))) |
| THM | hnot_greater_eq |
all( m:hnum. all( m:hnum. all( n:hnum. equal(not(ge(m,n)),le(suc(m),n)))) n:hnum. equal(not(ge(m,n)),le(suc(m),n)))) |
| THM | hsuc_one_add |
all( n:hnum. equal(suc(n),add(1,n))) n:hnum. equal(suc(n),add(1,n))) |
| THM | hsuc_add_sym |
all( m:hnum. all( m:hnum. all( n:hnum. equal(suc(add(m,n)),add(suc(n),m)))) n:hnum. equal(suc(add(m,n)),add(suc(n),m)))) |
| THM | hnot_suc_add_less_eq |
all( m:hnum. all( m:hnum. all( n:hnum. not(le(suc(add(m,n)),m)))) n:hnum. not(le(suc(add(m,n)),m)))) |
| THM | hmult_less_eq_suc |
all
( m:hnum. all m:hnum. all
( m:hnum. ( m:hnum. ( n:hnum. all n:hnum. all
( m:hnum. ( m:hnum. ( n:hnum. ( n:hnum. ( p:hnum. equal p:hnum. equal
( m:hnum. ( m:hnum. ( n:hnum. ( n:hnum. ( p:hnum. (le(m,n) p:hnum. (le(m,n)
( m:hnum. ( m:hnum. ( n:hnum. ( n:hnum. ( p:hnum. ,le(mult(suc(p),m),mult(suc(p),n)))))) p:hnum. ,le(mult(suc(p),m),mult(suc(p),n)))))) |
| THM | hsub_left_add |
all
( m:hnum. all m:hnum. all
( m:hnum. ( m:hnum. ( n:hnum. all n:hnum. all
( m:hnum. ( m:hnum. ( n:hnum. ( n:hnum. ( p:hnum. equal p:hnum. equal
( m:hnum. ( m:hnum. ( n:hnum. ( n:hnum. ( p:hnum. (add(m,sub(n,p)) p:hnum. (add(m,sub(n,p))
( m:hnum. ( m:hnum. ( n:hnum. ( n:hnum. ( p:hnum. ,cond(le(n,p),m,sub(add(m,n),p)))))) p:hnum. ,cond(le(n,p),m,sub(add(m,n),p)))))) |
| THM | hsub_right_add |
all
( m:hnum. all m:hnum. all
( m:hnum. ( m:hnum. ( n:hnum. all n:hnum. all
( m:hnum. ( m:hnum. ( n:hnum. ( n:hnum. ( p:hnum. equal p:hnum. equal
( m:hnum. ( m:hnum. ( n:hnum. ( n:hnum. ( p:hnum. (add(sub(m,n),p) p:hnum. (add(sub(m,n),p)
( m:hnum. ( m:hnum. ( n:hnum. ( n:hnum. ( p:hnum. ,cond(le(m,n),p,sub(add(m,p),n)))))) p:hnum. ,cond(le(m,n),p,sub(add(m,p),n)))))) |
| THM | hsub_left_sub |
all
( m:hnum. all m:hnum. all
( m:hnum. ( m:hnum. ( n:hnum. all n:hnum. all
( m:hnum. ( m:hnum. ( n:hnum. ( n:hnum. ( p:hnum. equal p:hnum. equal
( m:hnum. ( m:hnum. ( n:hnum. ( n:hnum. ( p:hnum. (sub(m,sub(n,p)) p:hnum. (sub(m,sub(n,p))
( m:hnum. ( m:hnum. ( n:hnum. ( n:hnum. ( p:hnum. ,cond(le(n,p),m,sub(add(m,p),n)))))) p:hnum. ,cond(le(n,p),m,sub(add(m,p),n)))))) |
| THM | hsub_right_sub |
all( m:hnum. all( m:hnum. all( n:hnum. all( n:hnum. all( p:hnum. equal(sub(sub(m,n),p),sub(m,add(n,p)))))) p:hnum. equal(sub(sub(m,n),p),sub(m,add(n,p)))))) |
| THM | hsub_left_suc |
all
( m:hnum. all( m:hnum. all( n:hnum. equal(suc(sub(m,n)),cond(le(m,n),suc(0),sub(suc(m),n))))) n:hnum. equal(suc(sub(m,n)),cond(le(m,n),suc(0),sub(suc(m),n))))) |
| THM | hsub_left_less_eq |
all
( m:hnum. all m:hnum. all
( m:hnum. ( m:hnum. ( n:hnum. all n:hnum. all
( m:hnum. ( m:hnum. ( n:hnum. ( n:hnum. ( p:hnum. equal p:hnum. equal
( m:hnum. ( m:hnum. ( n:hnum. ( n:hnum. ( p:hnum. (le(m,sub(n,p)) p:hnum. (le(m,sub(n,p))
( m:hnum. ( m:hnum. ( n:hnum. ( n:hnum. ( p:hnum. ,or(le(add(m,p),n),le(m,0)))))) p:hnum. ,or(le(add(m,p),n),le(m,0)))))) |
| THM | hsub_right_less_eq |
all( m:hnum. all( m:hnum. all( n:hnum. all( n:hnum. all( p:hnum. equal(le(sub(m,n),p),le(m,add(n,p)))))) p:hnum. equal(le(sub(m,n),p),le(m,add(n,p)))))) |
| THM | hsub_left_less |
all( m:hnum. all( m:hnum. all( n:hnum. all( n:hnum. all( p:hnum. equal(lt(m,sub(n,p)),lt(add(m,p),n))))) p:hnum. equal(lt(m,sub(n,p)),lt(add(m,p),n))))) |
| THM | hsub_right_less |
all
( m:hnum. all m:hnum. all
( m:hnum. ( m:hnum. ( n:hnum. all n:hnum. all
( m:hnum. ( m:hnum. ( n:hnum. ( n:hnum. ( p:hnum. equal p:hnum. equal
( m:hnum. ( m:hnum. ( n:hnum. ( n:hnum. ( p:hnum. (lt(sub(m,n),p) p:hnum. (lt(sub(m,n),p)
( m:hnum. ( m:hnum. ( n:hnum. ( n:hnum. ( p:hnum. ,and(lt(m,add(n,p)),lt(0,p)))))) p:hnum. ,and(lt(m,add(n,p)),lt(0,p)))))) |
| THM | hsub_left_greater_eq |
all( m:hnum. all( m:hnum. all( n:hnum. all( n:hnum. all( p:hnum. equal(ge(m,sub(n,p)),ge(add(m,p),n))))) p:hnum. equal(ge(m,sub(n,p)),ge(add(m,p),n))))) |
| THM | hsub_right_greater_eq |
all
( m:hnum. all m:hnum. all
( m:hnum. ( m:hnum. ( n:hnum. all n:hnum. all
( m:hnum. ( m:hnum. ( n:hnum. ( n:hnum. ( p:hnum. equal p:hnum. equal
( m:hnum. ( m:hnum. ( n:hnum. ( n:hnum. ( p:hnum. (ge(sub(m,n),p) p:hnum. (ge(sub(m,n),p)
( m:hnum. ( m:hnum. ( n:hnum. ( n:hnum. ( p:hnum. ,or(ge(m,add(n,p)),ge(0,p)))))) p:hnum. ,or(ge(m,add(n,p)),ge(0,p)))))) |
| THM | hsub_left_greater |
all
( m:hnum. all m:hnum. all
( m:hnum. ( m:hnum. ( n:hnum. all n:hnum. all
( m:hnum. ( m:hnum. ( n:hnum. ( n:hnum. ( p:hnum. equal p:hnum. equal
( m:hnum. ( m:hnum. ( n:hnum. ( n:hnum. ( p:hnum. (gt(m,sub(n,p)) p:hnum. (gt(m,sub(n,p))
( m:hnum. ( m:hnum. ( n:hnum. ( n:hnum. ( p:hnum. ,and(gt(add(m,p),n),gt(m,0)))))) p:hnum. ,and(gt(add(m,p),n),gt(m,0)))))) |
| THM | hsub_right_greater |
all( m:hnum. all( m:hnum. all( n:hnum. all( n:hnum. all( p:hnum. equal(gt(sub(m,n),p),gt(m,add(n,p)))))) p:hnum. equal(gt(sub(m,n),p),gt(m,add(n,p)))))) |
| THM | hsub_left_eq |
all
( m:hnum. all m:hnum. all
( m:hnum. ( m:hnum. ( n:hnum. all n:hnum. all
( m:hnum. ( m:hnum. ( n:hnum. ( n:hnum. ( p:hnum. equal p:hnum. equal
( m:hnum. ( m:hnum. ( n:hnum. ( n:hnum. ( p:hnum. (equal(m,sub(n,p)) p:hnum. (equal(m,sub(n,p))
( m:hnum. ( m:hnum. ( n:hnum. ( n:hnum. ( p:hnum. ,or(equal(add(m,p),n),and(le(m,0),le(n,p))))))) p:hnum. ,or(equal(add(m,p),n),and(le(m,0),le(n,p))))))) |
| THM | hsub_right_eq |
all
( m:hnum. all m:hnum. all
( m:hnum. ( m:hnum. ( n:hnum. all n:hnum. all
( m:hnum. ( m:hnum. ( n:hnum. ( n:hnum. ( p:hnum. equal p:hnum. equal
( m:hnum. ( m:hnum. ( n:hnum. ( n:hnum. ( p:hnum. (equal(sub(m,n),p) p:hnum. (equal(sub(m,n),p)
( m:hnum. ( m:hnum. ( n:hnum. ( n:hnum. ( p:hnum. ,or(equal(m,add(n,p)),and(le(m,n),le(p,0))))))) p:hnum. ,or(equal(m,add(n,p)),and(le(m,n),le(p,0))))))) |
| THM | suc_not |
 n: n: . . 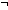 0 = n+1 0 = n+1 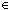  |
| THM | add_0 |
 m: m: . m+0 = m . m+0 = m 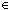  |
| THM | add_suc |
 m,n: m,n: . (m+n)+1 = m+(n+1) . (m+n)+1 = m+(n+1) 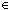  |
| THM | add_clauses |
 n,m: n,m: . 0+m = m . 0+m = m 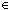  & m+0 = m & m+0 = m 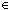  & m+1+n = m+n+1 & m+1+n = m+n+1 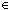  & m+(n+1) = (m+n)+1 & m+(n+1) = (m+n)+1 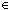  |
| THM | add_sym |
 m,n: m,n: . m+n = n+m . m+n = n+m 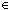  |
| THM | num_cases |
 m: m: . m = 0 . m = 0 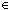  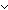 ( (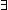 n: n: . m = n+1 . m = n+1 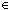  ) ) |
| THM | less_mono_rev |
 m,n: m,n: . m+1<n+1 . m+1<n+1 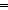 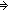 m<n m<n |
| THM | less_mono_eq |
 m,n: m,n: . m+1<n+1 . m+1<n+1 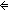 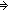 m<n m<n |
| THM | suc_sub1 |
 m: m: . nnsub(m+1;1) = m . nnsub(m+1;1) = m |
| THM | pre_sub1 |
 m: m: . pre(m) = nnsub(m;1) . pre(m) = nnsub(m;1) |
| THM | less_add |
 m,n: m,n: . n<m . n<m 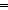 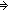 ( (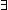 x: x: . x+n = m . x+n = m   ) ) |