Thm*  x,n,m: x,n,m: . x . x n & x n & x m m   (nnsub(n;x) = nnsub(m;x) (nnsub(n;x) = nnsub(m;x) 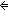  n = m) n = m) | [cancel_sub] |
Thm*  x,n,m: x,n,m: . n . n x & m x & m x x   (nnsub(x;n) = nnsub(x;m) (nnsub(x;n) = nnsub(x;m) 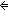  n = m) n = m) | [sub_cancel] |
Thm*  m,x: m,x: . m . m x x   ( ( n: n: . nnsub(x;m) . nnsub(x;m) n n 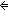  x x m+n) m+n) | [sub_less_eq_add] |
Thm*  b,c: b,c: . c . c b b   ( ( a: a: . nnsub(a;nnsub(b;c)) = nnsub(a+c;b)) . nnsub(a;nnsub(b;c)) = nnsub(a+c;b)) | [sub_sub] |
Thm*  a,b: a,b: . b . b a a   ( ( c: c: . nnsub(a;b)<c . nnsub(a;b)<c 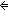  a<b+c) a<b+c) | [less_eq_sub_less] |
Thm*  c: c: . nnsub(c;c) = 0 . nnsub(c;c) = 0 | [sub_equal_0] |
Thm*  c,b: c,b: . c . c b b   ( ( a: a: . nnsub(a+b;c) = a+nnsub(b;c)) . nnsub(a+b;c) = a+nnsub(b;c)) | [less_eq_add_sub] |
Thm*  a,c: a,c: . nnsub(a+c;c) = a . nnsub(a+c;c) = a | [add_sub] |
Thm*  n,m,i: n,m,i: . i<nnsub(n;m) . i<nnsub(n;m)   i+m<n i+m<n | [less_sub_add_less] |
Thm*  m,n: m,n: . n<m . n<m   n n nnsub(m;1) nnsub(m;1) | [sub_less_or] |
Thm*  n,m: n,m: . m<n . m<n 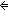  0<nnsub(n;m) 0<nnsub(n;m) | [sub_less_0] |
Thm*  m,n: m,n: . nnsub(m;n) = m . nnsub(m;n) = m 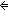  m = 0 m = 0 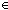  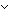 n = 0 n = 0 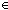  | [sub_eq_eq_0] |
Thm*  n,m: n,m: . nnsub(n;m) . nnsub(n;m) n n | [sub_less_eq] |
Thm*  a,b,c: a,b,c: . nnsub(a;b+c) = nnsub(nnsub(a;b);c) . nnsub(a;b+c) = nnsub(nnsub(a;b);c) | [sub_plus] |
Thm*  n,m: n,m: . nnsub(n+1;m+1) = nnsub(n;m) . nnsub(n+1;m+1) = nnsub(n;m) | [sub_mono_eq] |
Thm*  m,n,x: m,n,x: . x . x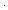 nnsub(m;n) = nnsub(x nnsub(m;n) = nnsub(x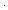 m;x m;x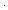 n) n) | [left_sub_distrib] |
Thm*  m,n,x: m,n,x: . nnsub(m;n) . nnsub(m;n)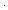 x = nnsub(m x = nnsub(m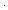 x;n x;n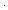 x) x) | [right_sub_distrib] |
Thm*  m,n,x: m,n,x: . n . n x x   (m+n = x (m+n = x 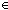  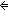  m = nnsub(x;n)) m = nnsub(x;n)) | [add_eq_sub] |
Thm*  m,n: m,n: . pre(nnsub(m;n)) = nnsub(pre(m);n) . pre(nnsub(m;n)) = nnsub(pre(m);n) | [pre_sub] |
Thm*  m,n: m,n: . n . n m m   nnsub(m;n)+n = m nnsub(m;n)+n = m 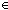  | [sub_add] |
Thm*  m,n: m,n: . nnsub(m;n) = 0 . nnsub(m;n) = 0 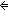  m m n n | [sub_eq_0] |
Thm*  m: m: . nnsub(0;m) = 0 & nnsub(m;0) = m . nnsub(0;m) = 0 & nnsub(m;0) = m | [sub_0] |