Thm*  'b,'a:S, x:('a 'b,'a:S, x:('a   'b). 'b).
Thm* ( x:'b. x) o x = x x:'b. x) o x = x 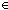 ('a ('a   'b) & x o ( 'b) & x o ( x:'a. x) = x x:'a. x) = x 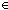 ('a ('a   'b) 'b) | [i_o_id] |
Thm*  'a:S, x:'a. x = x 'a:S, x:'a. x = x | [i_thm] |
Thm*  'a,'b,'c:S, x:('a 'a,'b,'c:S, x:('a   'b 'b   'c), x@0:('a 'c), x@0:('a   'b), x@1:'a. 'b), x@1:'a.
Thm* x(x@1,x@0(x@1)) = x(x@1,x@0(x@1)) | [s_thm] |
Thm*  'a,'b:S, x:'a, x@0:'b. x = x 'a,'b:S, x:'a, x@0:'b. x = x | [k_thm] |
Thm*  'a,'c,'d,'b:S, x:('c 'a,'c,'d,'b:S, x:('c   'd), x@0:('b 'd), x@0:('b   'c), x@1:('a 'c), x@1:('a   'b). 'b).
Thm* x o (x@0 o x@1) = (x o x@0) o x@1 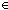 ('a ('a   'd) 'd) | [o_assoc] |
Thm*  'b,'c,'a:S, x:('b 'b,'c,'a:S, x:('b   'c), x@0:('a 'c), x@0:('a   'b), x@1:'a. 'b), x@1:'a.
Thm* (x o x@0)(x@1) = x(x@0(x@1)) | [o_thm] |
Thm*  'b,'a:S. all( 'b,'a:S. all( f:'a f:'a   'b. and(equal(o(i,f),f),equal(o(f,i),f))) 'b. and(equal(o(i,f),f),equal(o(f,i),f))) | [hi_o_id] |
Thm*  'a:S. all( 'a:S. all( x:'a. equal(i(x),x)) x:'a. equal(i(x),x)) | [hi_thm] |
Thm*  'a,'b,'c:S. 'a,'b,'c:S.
Thm* all
Thm* ( f:'a f:'a   'b 'b   'c. all 'c. all
Thm* ( f:'a f:'a   'b 'b   'c. ( 'c. ( g:'a g:'a   'b. all( 'b. all( x:'a. equal(s(f,g,x),f(x,g(x)))))) x:'a. equal(s(f,g,x),f(x,g(x)))))) | [hs_thm] |
Thm*  'a,'b:S. all( 'a,'b:S. all( x:'a. all( x:'a. all( y:'b. equal(k(x,y),x))) y:'b. equal(k(x,y),x))) | [hk_thm] |
Thm*  'a,'c,'d,'b:S. 'a,'c,'d,'b:S.
Thm* all
Thm* ( f:'c f:'c   'd. all 'd. all
Thm* ( f:'c f:'c   'd. ( 'd. ( g:'b g:'b   'c. all 'c. all
Thm* ( f:'c f:'c   'd. ( 'd. ( g:'b g:'b   'c. ( 'c. ( h:'a h:'a   'b. equal(o(f,o(g,h)),o(o(f,g),h))))) 'b. equal(o(f,o(g,h)),o(o(f,g),h))))) | [ho_assoc] |
Thm*  'b,'c,'a:S. 'b,'c,'a:S.
Thm* all( f:'b f:'b   'c. all( 'c. all( g:'a g:'a   'b. all( 'b. all( x:'a. equal(o(f,g,x),f(g(x)))))) x:'a. equal(o(f,g,x),f(g(x)))))) | [ho_thm] |
Thm*  'a:S. equal(i,s(k,k)) 'a:S. equal(i,s(k,k)) | [hi_def] |
Thm*  'c,'b,'a:S. equal(s, 'c,'b,'a:S. equal(s, f:'a f:'a   'b 'b   'c. 'c.  g:'a g:'a   'b. 'b.  x:'a. f(x,g(x))) x:'a. f(x,g(x))) | [hs_def] |
Thm*  'a,'b:S. equal(k, 'a,'b:S. equal(k, x:'a. x:'a.  y:'b. x) y:'b. x) | [hk_def] |
Thm*  'c,'b,'a:S. 'c,'b,'a:S.
Thm* all( f:'b f:'b   'c. all( 'c. all( g:'a g:'a   'b. equal(o(f,g), 'b. equal(o(f,g), x:'a. f(g(x))))) x:'a. f(g(x))))) | [ho_def] |