Thm*  'b,'a:S, x:'b, f:('b 'b,'a:S, x:'b, f:('b  'a 'a  ('a List) ('a List)  'b). 'b).
Thm* (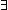 fn1:(('a List) fn1:(('a List)  'b). 'b).
Thm* (fn1(nil) = x & ( h:'a, t:'a List. fn1(cons(h; t)) = f(fn1(t),h,t))) h:'a, t:'a List. fn1(cons(h; t)) = f(fn1(t),h,t)))
Thm* & ( fn1,y:(('a List) fn1,y:(('a List)  'b). 'b).
Thm* & (fn1(nil) = x & ( h:'a, t:'a List. fn1(cons(h; t)) = f(fn1(t),h,t)) h:'a, t:'a List. fn1(cons(h; t)) = f(fn1(t),h,t))
Thm* & (& y(nil) = x
Thm* & (& ( h:'a, t:'a List. y(cons(h; t)) = f(y(t),h,t)) h:'a, t:'a List. y(cons(h; t)) = f(y(t),h,t))
Thm* & (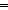 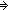
Thm* & (fn1 = y) | [list_axiom] |
Thm*  'b,'a:S. 'b,'a:S.
Thm* all
Thm* ( x:'b. all x:'b. all
Thm* ( x:'b. ( x:'b. ( f:'b f:'b
Thm* ( x:'b. ( x:'b. (  'a 'a
Thm* ( x:'b. ( x:'b. (  hlist('a) hlist('a)
Thm* ( x:'b. ( x:'b. (  'b. exists_unique 'b. exists_unique
Thm* ( x:'b. ( x:'b. (  'b. ( 'b. ( fn1:hlist('a) fn1:hlist('a)   'b. and 'b. and
Thm* ( x:'b. ( x:'b. (  'b. ( 'b. ( fn1:hlist('a) fn1:hlist('a)   'b. (equal(fn1(nil),x) 'b. (equal(fn1(nil),x)
Thm* ( x:'b. ( x:'b. (  'b. ( 'b. ( fn1:hlist('a) fn1:hlist('a)   'b. ,all 'b. ,all
Thm* ( x:'b. ( x:'b. (  'b. ( 'b. ( fn1:hlist('a) fn1:hlist('a)   'b. ,( 'b. ,( h:'a. all h:'a. all
Thm* ( x:'b. ( x:'b. (  'b. ( 'b. ( fn1:hlist('a) fn1:hlist('a)   'b. ,( 'b. ,( h:'a. ( h:'a. ( t:hlist('a). equal t:hlist('a). equal
Thm* ( x:'b. ( x:'b. (  'b. ( 'b. ( fn1:hlist('a) fn1:hlist('a)   'b. ,( 'b. ,( h:'a. ( h:'a. ( t:hlist('a). (fn1 t:hlist('a). (fn1
Thm* ( x:'b. ( x:'b. (  'b. ( 'b. ( fn1:hlist('a) fn1:hlist('a)   'b. ,( 'b. ,( h:'a. ( h:'a. ( t:hlist('a). ((cons(h,t)) t:hlist('a). ((cons(h,t))
Thm* ( x:'b. ( x:'b. (  'b. ( 'b. ( fn1:hlist('a) fn1:hlist('a)   'b. ,( 'b. ,( h:'a. ( h:'a. ( t:hlist('a). ,f t:hlist('a). ,f
Thm* ( x:'b. ( x:'b. (  'b. ( 'b. ( fn1:hlist('a) fn1:hlist('a)   'b. ,( 'b. ,( h:'a. ( h:'a. ( t:hlist('a). ,(fn1(t) t:hlist('a). ,(fn1(t)
Thm* ( x:'b. ( x:'b. (  'b. ( 'b. ( fn1:hlist('a) fn1:hlist('a)   'b. ,( 'b. ,( h:'a. ( h:'a. ( t:hlist('a). ,,h t:hlist('a). ,,h
Thm* ( x:'b. ( x:'b. (  'b. ( 'b. ( fn1:hlist('a) fn1:hlist('a)   'b. ,( 'b. ,( h:'a. ( h:'a. ( t:hlist('a). ,,t)))))))) t:hlist('a). ,,t)))))))) | [hlist_axiom] |