Selected Objects
| COM | INT_DEFS_acom |
Integer related definitions |
| COM | ge_gt_wf_com |
These wf lemmas are used by EqCD during rewriting to ensure that subterms come out in right order. |
| def | lelt |
i 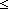 j < k == i j < k == i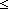 j & j<k j & j<k |
| def | lele |
i 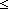 j j 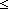 k == i k == i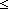 j & j j & j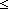 k k |
| def | nat |
 == {i: == {i: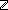 | 0 | 0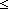 i } i } |
| def | nat_plus |
 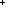 == {i: == {i: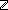 | 0<i } | 0<i } |
| THM | nat_plus_properties |
 i: i: 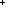 . 0<i . 0<i |
| def | int_nzero |
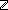  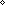 == {i: == {i: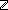 | i | i 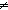 0 } 0 } |
| THM | int_nzero_properties |
 i: i: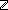  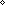 . i . i 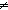 0 0 |
| def | int_upper |
{i...} == {j: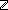 | i | i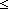 j } j } |
| THM | int_upper_properties |
 i: i: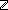 , j:{i...}. i , j:{i...}. i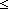 j j |
| def | int_lower |
{...i} == {j: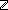 | j | j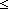 i } i } |
| THM | int_lower_properties |
 i: i: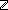 , j:{...i}. j , j:{...i}. j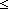 i i |
| def | int_seg |
{i..j } == {k: } == {k: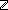 | i | i 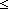 k < j } k < j } |
| THM | int_seg_properties |
 i,j: i,j: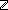 , y:{i..j , y:{i..j }. i }. i 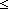 y < j y < j |
| THM | decidable__equal_int_seg |
 i,j: i,j: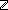 , x,y:{i..j , x,y:{i..j }. Dec(x = y) }. Dec(x = y) |
| def | int_iseg |
{i...j} == {k: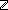 | i | i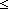 k & k k & k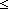 j } j } |
| THM | int_iseg_properties |
 i,j: i,j: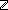 , y:{i...j}. i , y:{i...j}. i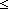 y & y y & y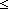 j j |
| THM | int_lt_to_int_upper |
 i: i: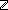 , A:({i+1...} , A:({i+1...} 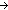 Prop). ( Prop). ( j: j: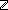 . i<j . i<j   A(j)) A(j)) 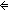  ( ( j:{i+1...}. A(j)) j:{i+1...}. A(j)) |
| THM | int_le_to_int_upper |
 i: i: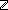 , A:({i...} , A:({i...} 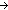 Prop). ( Prop). ( j: j: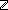 . i . i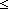 j j   A(j)) A(j)) 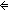  ( ( j:{i...}. A(j)) j:{i...}. A(j)) |
| COM | INT_INCLUSIONS_tcom |
Inclusion relations between integer subypes |
| COM | INDUCTION_tcom |
Induction over naturals
... |
| THM | nat_ind_a |
 P:( P:(  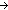 Prop). P(0) Prop). P(0)   ( ( i: i: 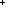 . P(i-1) . P(i-1)   P(i)) P(i))   ( ( i: i: . P(i)) . P(i)) |
| THM | nat_ind_tp |
 P:( P:(  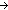 Prop). P(0) Prop). P(0)   ( ( i: i: 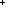 . P(i-1) . P(i-1)   P(i)) P(i))   ( ( i: i: . P(i)) . P(i)) |
| THM | nat_ind |
 P:( P:(  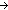 Prop). P(0) Prop). P(0)   ( ( i: i: 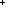 . P(i-1) . P(i-1)   P(i)) P(i))   ( ( j: j: . P(j)) . P(j)) |
| THM | comp_nat_ind_tp |
 P:( P:(  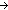 Prop). ( Prop). ( i: i: . ( . ( j: j: . j<i . j<i   P(j)) P(j))   P(i)) P(i))   ( ( i: i: . P(i)) . P(i)) |
| THM | comp_nat_ind_a |
 P:( P:(  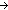 Prop). ( Prop). ( i: i: . ( . ( j: j: . j<i . j<i   P(j)) P(j))   P(i)) P(i))   ( ( i: i: . P(i)) . P(i)) |
| THM | nat_well_founded |
WellFnd{i}( ;x,y.x<y) ;x,y.x<y) |
| COM | OLD_INDUCTION |
|
| THM | complete_nat_ind |
 P:( P:(  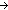 Prop). ( Prop). ( i: i: . ( . ( j: j: i. P(j)) i. P(j))   P(i)) P(i))   ( ( i: i: . P(i)) . P(i)) |
| def | suptype |
S 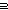 T == T T == T 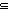 S S |
| THM | complete_nat_ind_with_y |
 P:( P:(  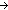 Prop). ( Prop). ( i: i: . ( . ( j: j: i. P(j)) i. P(j))   P(i)) P(i))   ( ( i: i: . P(i)) . P(i)) |