Thm*  i,j: i,j: , F:({i..j , F:({i..j } } 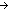 Prop). ( Prop). ( k:{i..j k:{i..j }. Dec(F(k))) }. Dec(F(k)))   Dec( Dec( k:{i..j k:{i..j }. F(k)) }. F(k)) | [decidable__all_int_seg] |
Thm*  i,j: i,j: , F:({i..j , F:({i..j } } 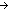 Prop). ( Prop). ( k:{i..j k:{i..j }. Dec(F(k))) }. Dec(F(k)))   Dec( Dec(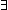 k:{i..j k:{i..j }. F(k)) }. F(k)) | [decidable__ex_int_seg] |
Thm*  i,j: i,j: . .
Thm* i<j
Thm*  
Thm* ( F:({i..j F:({i..j } } 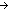 Prop). ( Prop). ( k:{i..j k:{i..j }. F(k)) }. F(k))   F(i) & ( F(i) & ( k:{(i+1)..j k:{(i+1)..j }. F(k))) }. F(k))) | [split_int_seg_all_dom_sfa] |
Thm*  i,j: i,j: . .
Thm* i<j
Thm*  
Thm* ( F:({i..j F:({i..j } } 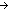 Prop). ( Prop). (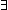 k:{i..j k:{i..j }. F(k)) }. F(k))   F(i) F(i) 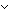 ( (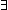 k:{(i+1)..j k:{(i+1)..j }. F(k))) }. F(k))) | [split_int_seg_exist_dom_sfa] |
Thm*  i: i: , j:{i...}. WellFnd{u}({i..j , j:{i...}. WellFnd{u}({i..j };x,y.x>y) };x,y.x>y) | [int_seg_well_founded_down] |
Thm*  i: i: , j:{i+1...}, E:({i..j , j:{i+1...}, E:({i..j } } 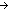 Prop). Prop).
Thm* E(i)   ( ( k:{(i+1)..j k:{(i+1)..j }. E(k-1) }. E(k-1)   E(k)) E(k))   ( ( k:{i..j k:{i..j }. E(k)) }. E(k)) | [int_seg_ind] |
Thm*  i: i: , j:{i...}. WellFnd{u}({i..j , j:{i...}. WellFnd{u}({i..j };x,y.x<y) };x,y.x<y) | [int_seg_well_founded_up] |
Thm*  a: a: , n:{...-1}. (a rem n) , n:{...-1}. (a rem n)   (-n) (-n) | [rem_bounds_4_typing_sfa] |
Thm*  a:{...0}, n:{...-1}. -(a rem n) a:{...0}, n:{...-1}. -(a rem n)   (-n) (-n) | [rem_bounds_3_typing_sfa] |
Thm*  a:{...0}, n: a:{...0}, n:  . -(a rem n) . -(a rem n)   n n | [rem_bounds_2_typing_sfa] |
Thm*  a: a: , n: , n:  . (a rem n) . (a rem n)   n n | [rem_bounds_1_typing_sfa] |
Thm*  k: k:  , r1,r2: , r1,r2: k, q1,q2: k, q1,q2: . q1 . q1 k-r1 k-r1 q2 q2 k-r2 k-r2   q1 q1 q2 q2 | [division_mono2_sfa] |
Thm*  k: k:  , r1,r2: , r1,r2: k, q1,q2: k, q1,q2: . q1 . q1 k+r1 k+r1 q2 q2 k+r2 k+r2   q1 q1 q2 q2 | [division_mono1_sfa] |
Thm*  k: k:  , r1,r2: , r1,r2: k, q1,q2: k, q1,q2: . .
Thm* q1 k+r1 = q2 k+r1 = q2 k-r2 k-r2   q1 = q2 & r1 = 0 & r2 = 0 q1 = q2 & r1 = 0 & r2 = 0 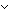 q2 = q1+1 & r2 = k-r1 q2 = q1+1 & r2 = k-r1 | [division4_sfa] |
Thm*  k: k:  , r1,r2: , r1,r2: k, q1,q2: k, q1,q2: . q1 . q1 k-r1 = -(q2 k-r1 = -(q2 k+r2) k+r2)   q1 = -q2 & r1 = r2 q1 = -q2 & r1 = r2 | [division3_sfa] |
Thm*  k: k:  , r1,r2: , r1,r2: k, q1,q2: k, q1,q2: . q1 . q1 k-r1 = q2 k-r1 = q2 k-r2 k-r2   q1 = q2 & r1 = r2 q1 = q2 & r1 = r2 | [division2_sfa] |
Thm*  k: k:  , r1,r2: , r1,r2: k, q1,q2: k, q1,q2: . q1 . q1 k+r1 = q2 k+r1 = q2 k+r2 k+r2   q1 = q2 & r1 = r2 q1 = q2 & r1 = r2 | [division1_sfa] |