Selected Objects
| Introduction | Introductory Remarks |
| COM | int_2_begin |
Reworked (sfa) version of int_2.
... |
| THM | lt_to_le_rw |
 i,j: i,j: . i<j . i<j   i+1 i+1 j j |
| THM | le_to_lt_rw |
 i,j: i,j: . i . i j j   i<j+1 i<j+1 |
| THM | add_mono_wrt_eq_rw |
 a,b,n: a,b,n: . a = b . a = b   a+n = b+n a+n = b+n |
| THM | add_mono_wrt_lt_rw |
 a,b,n: a,b,n: . a<b . a<b   a+n<b+n a+n<b+n |
| THM | add_mono_wrt_le_rw |
 a,b,n: a,b,n: . a . a b b   a+n a+n b+n b+n |
| THM | zero_ann_a |
 a,b: a,b: . a = 0 . a = 0 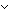 b = 0 b = 0   a a b = 0 b = 0 |
| THM | zero_ann_b |
 a,b: a,b: . . 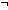 a a b = 0 b = 0   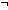 a = 0 & a = 0 & 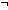 b = 0 b = 0 |
| THM | mul_preserves_le |
 a,b: a,b: , n: , n: . a . a b b   n n a a n n b b |
| THM | mul_preserves_lt |
 a,b: a,b: , n: , n:  . a<b . a<b   n n a<n a<n b b |
| THM | mul_cancel_in_le |
 a,b: a,b: , n: , n:  . n . n a a n n b b   a a b b |
| THM | mul_cancel_in_eq |
 a,b: a,b: , n: , n:  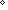 . n . n a = n a = n b b   a = b a = b |
| THM | mul_cancel_in_lt |
 a,b: a,b: , n: , n:  . n . n a<n a<n b b   a<b a<b |
| THM | multiply_functionality_wrt_le |
 i1,i2,j1,j2: i1,i2,j1,j2: . i1 . i1 j1 j1   i2 i2 j2 j2   i1 i1 i2 i2 j1 j1 j2 j2 |
| THM | int_entire |
 a,b: a,b: . a . a b = 0 b = 0   a = 0 a = 0 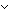 b = 0 b = 0 |
| THM | int_entire_a |
 a,b: a,b: . a . a  0 0   b b  0 0   a a b b  0 0 |
| THM | mul_bounds_1a |
 a,b: a,b: . 0 . 0 a a b b |
| THM | mul_bounds_1b |
 a,b: a,b:  . 0<a . 0<a b b |
| THM | pos_mul_arg_bounds |
 a,b: a,b: . a . a b>0 b>0   a>0 & b>0 a>0 & b>0 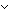 a<0 & b<0 a<0 & b<0 |
| THM | neg_mul_arg_bounds |
 a,b: a,b: . a . a b<0 b<0   a<0 & b>0 a<0 & b>0 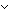 a>0 & b<0 a>0 & b<0 |
| COM | add_nat_wf_com |
It is a bad idea to make these usual wf lemmas since often one mixes integer funs and nat funs.
... |
| COM | quasi_lin_com |
======================
QUASI-LINEAR FUNCTIONS
====================== |
| def | absval |
|i| == if 0 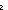 i i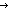 i else -i fi i else -i fi |
| THM | absval_pos |
 i: i: . |i| = i . |i| = i |
| THM | absval_neg |
 i:{...0}. |i| = -i i:{...0}. |i| = -i |
| def | pm_equal |
i = 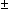 j == i = j j == i = j   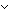 i = -j i = -j |
| THM | absval_zero |
 i: i: . |i| = 0 . |i| = 0   i = 0 i = 0 |
| THM | absval_ubound |
 i: i: , n: , n: . |i| . |i| n n   -n -n i & i i & i n n |
| THM | absval_lbound |
 i: i: , n: , n: . |i|>n . |i|>n   i<-n i<-n 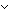 i>n i>n |
| THM | absval_eq |
 x,y: x,y: . |x| = |y| . |x| = |y|   x = x = 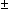 y y |
| THM | absval_sym |
 i: i: . |i| = |-i| . |i| = |-i| |
| THM | absval_elim |
 P:( P:(  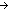 Prop). ( Prop). ( x: x: . P(|x|)) . P(|x|))   ( ( x: x: . P(x)) . P(x)) |
| def | imax |
imax(a;b) == if a 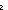 b b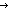 b else a fi b else a fi |
| def | imin |
imin(a;b) == if a 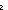 b b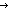 a else b fi a else b fi |
| THM | minus_imax |
 a,b: a,b: . -imax(a;b) = imin(-a;-b) . -imax(a;b) = imin(-a;-b) |
| THM | minus_imin |
 a,b: a,b: . -imin(a;b) = imax(-a;-b) . -imin(a;b) = imax(-a;-b) |
| THM | imax_lb |
 a,b,c: a,b,c: . imax(a;b) . imax(a;b) c c   a a c & b c & b c c |
| THM | imax_ub |
 a,b,c: a,b,c: . a . a imax(b;c) imax(b;c)   a a b b 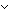 a a c c |
| THM | imax_add_r |
 a,b,c: a,b,c: . imax(a;b)+c = imax(a+c;b+c) . imax(a;b)+c = imax(a+c;b+c) |
| THM | imax_assoc |
 a,b,c: a,b,c: . imax(a;imax(b;c)) = imax(imax(a;b);c) . imax(a;imax(b;c)) = imax(imax(a;b);c) |
| THM | imax_com |
 a,b: a,b: . imax(a;b) = imax(b;a) . imax(a;b) = imax(b;a) |
| THM | imin_assoc |
 a,b,c: a,b,c: . imin(a;imin(b;c)) = imin(imin(a;b);c) . imin(a;imin(b;c)) = imin(imin(a;b);c) |
| THM | imin_com |
 a,b: a,b: . imin(a;b) = imin(b;a) . imin(a;b) = imin(b;a) |
| THM | imin_add_r |
 a,b,c: a,b,c: . imin(a;b)+c = imin(a+c;b+c) . imin(a;b)+c = imin(a+c;b+c) |
| THM | imin_lb |
 a,b,c: a,b,c: . imin(a;b) . imin(a;b) c c   a a c c 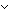 b b c c |
| THM | imin_ub |
 a,b,c: a,b,c: . a . a imin(b;c) imin(b;c)   a a b & a b & a c c |
| def | ndiff |
a -- b == imax(a-b;0) |
| THM | ndiff_id_r |
 a: a: . (a -- 0) = a . (a -- 0) = a |
| THM | ndiff_ann_l |
 a: a: . (0 -- a) = 0 . (0 -- a) = 0 |
| THM | ndiff_inv |
 a: a: , b: , b: . ((a+b) -- b) = a . ((a+b) -- b) = a |
| THM | ndiff_ndiff |
 a,b: a,b: , c: , c: . ((a -- b) -- c) = (a -- (b+c)) . ((a -- b) -- c) = (a -- (b+c)) |
| THM | ndiff_ndiff_eq_imin |
 a,b: a,b: . (a -- (a -- b)) = imin(a;b) . (a -- (a -- b)) = imin(a;b) |
| THM | ndiff_add_eq_imax |
 a,b: a,b: . (a -- b)+b = imax(a;b) . (a -- b)+b = imax(a;b) |
| THM | ndiff_zero |
 a,b: a,b: . (a -- b) = 0 . (a -- b) = 0   a a b b |
| COM | div_rem_com |
================================
DIVISION AND REMAINDER FUNCTIONS
================================ |
| THM | division1_sfa |
 k: k:  , r1,r2: , r1,r2: k, q1,q2: k, q1,q2: . q1 . q1 k+r1 = q2 k+r1 = q2 k+r2 k+r2   q1 = q2 & r1 = r2 q1 = q2 & r1 = r2 |
| THM | division2_sfa |
 k: k:  , r1,r2: , r1,r2: k, q1,q2: k, q1,q2: . q1 . q1 k-r1 = q2 k-r1 = q2 k-r2 k-r2   q1 = q2 & r1 = r2 q1 = q2 & r1 = r2 |
| THM | division3_sfa |
 k: k:  , r1,r2: , r1,r2: k, q1,q2: k, q1,q2: . q1 . q1 k-r1 = -(q2 k-r1 = -(q2 k+r2) k+r2)   q1 = -q2 & r1 = r2 q1 = -q2 & r1 = r2 |
| THM | division4_sfa |
 k: k:  , r1,r2: , r1,r2: k, q1,q2: k, q1,q2: . .
q1 k+r1 = q2 k+r1 = q2 k-r2 k-r2   q1 = q2 & r1 = 0 & r2 = 0 q1 = q2 & r1 = 0 & r2 = 0 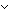 q2 = q1+1 & r2 = k-r1 q2 = q1+1 & r2 = k-r1 |
| THM | division_mono1_sfa |
 k: k:  , r1,r2: , r1,r2: k, q1,q2: k, q1,q2: . q1 . q1 k+r1 k+r1 q2 q2 k+r2 k+r2   q1 q1 q2 q2 |
| THM | division_mono2_sfa |
 k: k:  , r1,r2: , r1,r2: k, q1,q2: k, q1,q2: . q1 . q1 k-r1 k-r1 q2 q2 k-r2 k-r2   q1 q1 q2 q2 |
| THM | div_rem_sum |
 a: a: , n: , n:  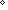 . a = (a . a = (a  n) n) n+(a rem n) n+(a rem n) |
| THM | rem_to_div |
 a: a: , n: , n:  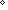 . (a rem n) = a-(a . (a rem n) = a-(a  n) n) n n |
| COM | quadrants_com |
Quadrants for a rem b and a  b are numbered as follows:
... b are numbered as follows:
... |
| THM | rem_bounds_1 |
 a: a: , n: , n:  . 0 . 0 (a rem n) & (a rem n)<n (a rem n) & (a rem n)<n |
| THM | rem_bounds_2 |
 a:{...0}, n: a:{...0}, n:  . 0 . 0 (a rem n) & (a rem n)>-n (a rem n) & (a rem n)>-n |
| THM | rem_bounds_3 |
 a:{...0}, n:{...-1}. 0 a:{...0}, n:{...-1}. 0 (a rem n) & (a rem n)>n (a rem n) & (a rem n)>n |
| THM | rem_bounds_4 |
 a: a: , n:{...-1}. 0 , n:{...-1}. 0 (a rem n) & (a rem n)<-n (a rem n) & (a rem n)<-n |
| THM | rem_bounds_1_typing_sfa |
 a: a: , n: , n:  . (a rem n) . (a rem n)   n n |
| THM | rem_bounds_2_typing_sfa |
 a:{...0}, n: a:{...0}, n:  . -(a rem n) . -(a rem n)   n n |
| THM | rem_bounds_3_typing_sfa |
 a:{...0}, n:{...-1}. -(a rem n) a:{...0}, n:{...-1}. -(a rem n)   (-n) (-n) |
| THM | rem_bounds_4_typing_sfa |
 a: a: , n:{...-1}. (a rem n) , n:{...-1}. (a rem n)   (-n) (-n) |
| THM | rem_sym |
 a: a: , b: , b:  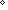 . (a rem -b) = (a rem b) . (a rem -b) = (a rem b) |
| THM | rem_antisym |
 a: a: , b: , b:  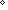 . ((-a) rem b) = -(a rem b) . ((-a) rem b) = -(a rem b) |
| THM | div_2_to_1 |
 a:{...0}, b: a:{...0}, b:  . (a . (a  b) = -((-a) b) = -((-a)  b) b) |
| THM | div_3_to_1 |
 a:{...0}, b:{...-1}. (a a:{...0}, b:{...-1}. (a  b) = ((-a) b) = ((-a)  (-b)) (-b)) |
| THM | div_4_to_1 |
 a: a: , b:{...-1}. (a , b:{...-1}. (a  b) = -(a b) = -(a  (-b)) (-b)) |
| THM | division_typing1a_sfa |
 a: a: , n: , n:  . (a . (a  n) n)   |
| THM | division_typing2a_sfa |
 a:{...0}, n:{...-1}. (a a:{...0}, n:{...-1}. (a  n) n)   |
| THM | division_typing1b_sfa |
 a:{...0}, n: a:{...0}, n:  . (a . (a  n) n)  {...0} {...0} |
| THM | division_typing2b_sfa |
 a: a: , n:{...-1}. (a , n:{...-1}. (a  n) n)  {...0} {...0} |
| THM | rem_2_to_1 |
 a:{...0}, n: a:{...0}, n:  . (a rem n) = -((-a) rem n) . (a rem n) = -((-a) rem n) |
| THM | rem_3_to_1 |
 a:{...0}, n:{...-1}. (a rem n) = -((-a) rem -n) a:{...0}, n:{...-1}. (a rem n) = -((-a) rem -n) |
| THM | rem_4_to_1 |
 a: a: , n:{...-1}. (a rem n) = (a rem -n) , n:{...-1}. (a rem n) = (a rem -n) |
| THM | rem_bounds_z |
 a: a: , b: , b:  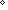 . |a rem b|<|b| . |a rem b|<|b| |
| THM | rem_sym_1 |
 a: a: , n: , n:  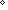 . -(a rem n) = ((-a) rem n) . -(a rem n) = ((-a) rem n) |
| THM | rem_sym_1a |
 a: a: , n: , n:  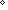 . (a rem n) = -((-a) rem n) . (a rem n) = -((-a) rem n) |
| THM | rem_sym_2 |
 a: a: , n: , n:  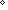 . (a rem n) = (a rem -n) . (a rem n) = (a rem -n) |
| THM | rem_mag_bound |
 a: a: , n: , n:  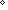 . |a rem n|<|n| . |a rem n|<|n| |
| THM | div_bounds_1 |
 a: a: , n: , n:  . 0 . 0 (a (a  n) n) |
| def | div_nrel |
Div(a;n;q) == n q q  a < n a < n (q+1) (q+1) |
| THM | div_fun_sat_div_nrel |
 a: a: , n: , n:  . Div(a;n;a . Div(a;n;a  n) n) |
| THM | div_elim |
 a: a: , n: , n:  . . 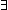 q: q: . Div(a;n;q) & (a . Div(a;n;q) & (a  n) = q n) = q |
| THM | div_unique |
 a: a: , n: , n:  , p,q: , p,q: . Div(a;n;p) . Div(a;n;p)   Div(a;n;q) Div(a;n;q)   p = q p = q |
| THM | div_lbound_1 |
 a: a: , n: , n:  , k: , k: . k . k (a (a  n) n)   k k n n a a |
| def | rem_nrel |
Rem(a;n;r) == 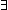 q: q: . Div(a;n;q) & q . Div(a;n;q) & q n+r = a n+r = a |
| THM | rem_fun_sat_rem_nrel |
 a: a: , n: , n:  . Rem(a;n;a rem n) . Rem(a;n;a rem n) |
| THM | div_base_case |
 a: a: , n: , n:  . a<n . a<n   (a (a  n) = 0 n) = 0 |
| THM | div_rec_case |
 a: a: , n: , n:  . a . a n n   (a (a  n) = ((a-n) n) = ((a-n)  n)+1 n)+1 |
| THM | rem_base_case |
 a: a: , n: , n:  . a<n . a<n   (a rem n) = a (a rem n) = a |
| THM | rem_gen_base_case |
 a: a: , n: , n:  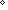 . |a|<|n| . |a|<|n|   (a rem n) = a (a rem n) = a |
| THM | rem_rec_case |
 a: a: , n: , n:  . a . a n n   (a rem n) = ((a-n) rem n) (a rem n) = ((a-n) rem n) |
| THM | rem_invariant |
 a,b: a,b: , n: , n:  . ((a+b . ((a+b n) rem n) = (a rem n) n) rem n) = (a rem n) |
| THM | rem_addition |
 i,j: i,j: , n: , n:  . (((i rem n)+(j rem n)) rem n) = ((i+j) rem n) . (((i rem n)+(j rem n)) rem n) = ((i+j) rem n) |
| THM | rem_rem_to_rem |
 a: a: , n: , n:  . ((a rem n) rem n) = (a rem n) . ((a rem n) rem n) = (a rem n) |
| THM | rem_base_case_z |
 a: a: , b: , b:  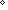 . |a|<|b| . |a|<|b|   (a rem b) = a (a rem b) = a |
| THM | rem_eq_args |
 a: a:  . (a rem a) = 0 . (a rem a) = 0 |
| THM | rem_eq_args_z |
 a: a: , b: , b:  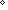 . |a| = |b| . |a| = |b|   (a rem b) = 0 (a rem b) = 0 |
| def | modulus |
a mod n == if 0 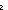 a a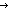 a rem n ; ((-a) rem n)= a rem n ; ((-a) rem n)=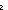 0 0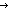 0 else n-((-a) rem n) fi 0 else n-((-a) rem n) fi |
| def | div_floor |
a  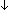 n == if 0 n == if 0 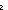 a a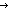 a a  n ; ((-a) rem n)= n ; ((-a) rem n)=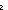 0 0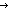 -((-a) -((-a)  n) else -((-a) n) else -((-a)  n)+-1 fi n)+-1 fi |
| THM | mod_bounds |
 a: a: , n: , n:  . 0 . 0 (a mod n) & (a mod n)<n (a mod n) & (a mod n)<n |
| THM | div_floor_mod_sum |
 a: a: , n: , n:  . a = (a . a = (a  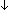 n) n) n+(a mod n) n+(a mod n) |
| THM | int_mag_well_founded |
WellFnd{i}( ;x,y.|x|<|y|) ;x,y.|x|<|y|) |
| THM | int_upper_well_founded |
 n: n: . WellFnd{i}({n...};x,y.x<y) . WellFnd{i}({n...};x,y.x<y) |
| THM | int_upper_ind |
 i: i: , E:({i...} , E:({i...} 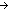 Prop). Prop).
E(i)   ( ( k:{i+1...}. E(k-1) k:{i+1...}. E(k-1)   E(k)) E(k))   ( ( k:{i...}. E(k)) k:{i...}. E(k)) |
| THM | int_lower_well_founded |
 n: n: . WellFnd{i}({...n};x,y.x>y) . WellFnd{i}({...n};x,y.x>y) |
| THM | int_lower_ind |
 i: i: , E:({...i} , E:({...i} 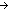 Prop). Prop).
E(i)   ( ( k:{...i-1}. E(k+1) k:{...i-1}. E(k+1)   E(k)) E(k))   ( ( k:{...i}. E(k)) k:{...i}. E(k)) |
| THM | int_seg_well_founded_up |
 i: i: , j:{i...}. WellFnd{u}({i..j , j:{i...}. WellFnd{u}({i..j };x,y.x<y) };x,y.x<y) |
| THM | int_seg_ind |
 i: i: , j:{i+1...}, E:({i..j , j:{i+1...}, E:({i..j } } 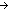 Prop). Prop).
E(i)   ( ( k:{(i+1)..j k:{(i+1)..j }. E(k-1) }. E(k-1)   E(k)) E(k))   ( ( k:{i..j k:{i..j }. E(k)) }. E(k)) |
| THM | int_seg_well_founded_down |
 i: i: , j:{i...}. WellFnd{u}({i..j , j:{i...}. WellFnd{u}({i..j };x,y.x>y) };x,y.x>y) |
| THM | split_int_seg_exist_dom_sfa |
 i,j: i,j: . .
i<j   ( ( F:({i..j F:({i..j } } 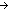 Prop). ( Prop). (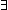 k:{i..j k:{i..j }. F(k)) }. F(k))   F(i) F(i) 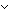 ( (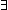 k:{(i+1)..j k:{(i+1)..j }. F(k))) }. F(k))) |
| THM | split_int_seg_all_dom_sfa |
 i,j: i,j: . .
i<j   ( ( F:({i..j F:({i..j } } 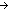 Prop). ( Prop). ( k:{i..j k:{i..j }. F(k)) }. F(k))   F(i) & ( F(i) & ( k:{(i+1)..j k:{(i+1)..j }. F(k))) }. F(k))) |
| THM | decidable__ex_int_seg |
 i,j: i,j: , F:({i..j , F:({i..j } } 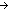 Prop). ( Prop). ( k:{i..j k:{i..j }. Dec(F(k))) }. Dec(F(k)))   Dec( Dec(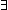 k:{i..j k:{i..j }. F(k)) }. F(k)) |
| THM | decidable__all_int_seg |
 i,j: i,j: , F:({i..j , F:({i..j } } 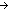 Prop). ( Prop). ( k:{i..j k:{i..j }. Dec(F(k))) }. Dec(F(k)))   Dec( Dec( k:{i..j k:{i..j }. F(k)) }. F(k)) |