Some proofs and tactics were added; many proofs were redone. See int 2 changes.

The well-formedness thm objects named remainder_wf, divide_wf, and divide_wfa were removed because they interfered with typing by the auto tactics. Here are the statements of those thms.
a:, n:. (a rem n)  
a:, n:. (a  n)  
a:, n:. (a  n)  

The objects named int_2_summary, mul_fun_comment, and absval_eval were removed because they are apparently otiose.

Here are the theorems added by sfa:

1.	Thm* k:, r1,r2:k, q1,q2:. q1k+r1 = q2k+r2  q1 = q2 & r1 = r2
2.	Thm* k:, r1,r2:k, q1,q2:. q1k-r1 = q2k-r2  q1 = q2 & r1 = r2
3.	Thm* k:, r1,r2:k, q1,q2:. q1k-r1 = -(q2k+r2)  q1 = -q2 & r1 = r2
4.	Thm* k:, r1,r2:k, q1,q2:. Thm* q1k+r1 = q2k-r2  q1 = q2 & r1 = 0 & r2 = 0  q2 = q1+1 & r2 = k-r1
5.	Thm* k:, r1,r2:k, q1,q2:. q1k+r1q2k+r2  q1q2
6.	Thm* k:, r1,r2:k, q1,q2:. q1k-r1q2k-r2  q1q2
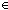
7.	Thm* a:, n:. (a rem n)  n
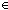
8.	Thm* a:{...0}, n:. -(a rem n)  n
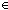
9.	Thm* a:{...0}, n:{...-1}. -(a rem n)  (-n)
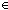
10.	Thm* a:, n:{...-1}. (a rem n)  (-n)
11.	Thm* a:, n:. (a  n)
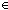
12.	Thm* a:{...0}, n:{...-1}. (a  n)
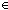
13.	Thm* a:{...0}, n:. (a  n)  {...0}
14.	Thm* a:, n:{...-1}. (a  n)  {...0}
15.	Thm* i,j:. Thm* i<j Thm*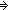  Thm* (F:({i..j}Prop). (k:{i..j}. F(k))  F(i)  (k:{(i+1)..j}. F(k)))
16.	Thm* i,j:. Thm* i<j Thm*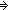  Thm* (F:({i..j}Prop). (k:{i..j}. F(k))  F(i) & (k:{(i+1)..j}. F(k)))

1 is the basic characterization of division with non-negative remainder. Also added were 2-4, as simple variants about sign change.

5 and 6 are basic facts about monotonicity of quotient.

7-14 stipulate ranges via types for the primitive remainder and quotient functions of Nuprl.

15 and 16 are rewrite lemmas for splitting off the low end of the indicated domain of quantification.

Some tactics were defined in objects absval_ML, imaxmin_sfa_ML, and division_sfa_ML.

ElimAbsVal and ElimImaxmin replace instances |x|, imin(a;b), and imax(a;b) by appropriate simplifications when they are easily determined. For example, ElimAbsVal would replace |x| by -x if x was obviously negative. Instances of imin(a;b) and imax(a;b) are replaced by "a" or "b" as appropriate, when it is easy to determine.

BoundRem will insert range typings for instances of (a rem b) when they are easily determined. ElaborateDivision will instantiate

Thm* a:, n:. a = (a  n)n+(a rem n)

on any instances of (a  b) or (a rem b), and then apply BoundRem.

About: IF YOU CAN SEE THIS go to /sfa/Nuprl/Shared/Xindentation_hack_doc.html