An occasion arose for review (by sfa ) of the proofs of the standard int_2 library, many of which were found to be needlessly long or otherwise difficult to follow. An indication of which theorems were added and which well-formedness theorems were deleted may be found in int 2 begin.

Some proofs involving |x|, imax(a;b), or imin(a;b) were reworked using new tacitics ElimAbsVal and ElimImaxmin, which eliminate these operators by simplifying them when the conditions for eliminating them are obvious to the auto tactics.

More radical changes were made to various proofs about integer division. The main plan was to reduce results rapidly to this fundamental abstract fact about division:

Thm* k:, r1,r2:k, q1,q2:. q1k+r1 = q2k+r2  q1 = q2 & r1 = r2

The "interface" between this lemma and the Nuprl primitive operators "a  b" and "a rem b" is effected by the following basic lemmas about concrete division, via the new tactics ElaborateDivision and BoundRem:

Thm* a:, n:. a = (a  n)n+(a rem n)

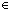
Thm* a:, n:. (a rem n)  n
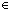
Thm* a:{...0}, n:. -(a rem n)  n
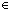
Thm* a:{...0}, n:{...-1}. -(a rem n)  (-n)
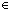
Thm* a:, n:{...-1}. (a rem n)  (-n)

ElaborateDivision will instantiate the first one on occurrences of "a  b" and "a rem b", then try BoundRem.
BoundRem will instantiate the last four lemmas when obvious.

See contrasting int 2 theorems for links to the old proofs of selected theorems exemplifying differences.

About: IF YOU CAN SEE THIS go to /sfa/Nuprl/Shared/Xindentation_hack_doc.html