Thm*  a: a: , n: , n:  . (a mod n) . (a mod n)   | [modulus_wf] |
Thm*  a: a: , n: , n:  . ((a rem n) rem n) = (a rem n) . ((a rem n) rem n) = (a rem n) | [rem_rem_to_rem] |
Thm*  i,j: i,j: , n: , n:  . (((i rem n)+(j rem n)) rem n) = ((i+j) rem n) . (((i rem n)+(j rem n)) rem n) = ((i+j) rem n) | [rem_addition] |
Thm*  a,b: a,b: , n: , n:  . ((a+b . ((a+b n) rem n) = (a rem n) n) rem n) = (a rem n) | [rem_invariant] |
Thm*  a: a: , n: , n:  . a . a n n   (a rem n) = ((a-n) rem n) (a rem n) = ((a-n) rem n) | [rem_rec_case] |
Thm*  a: a: , n: , n:  . a<n . a<n   (a rem n) = a (a rem n) = a | [rem_base_case] |
Thm*  a: a: , n: , n:  . a . a n n   (a (a  n) = ((a-n) n) = ((a-n)  n)+1 n)+1 | [div_rec_case] |
Thm*  a: a: , n: , n:  . a<n . a<n   (a (a  n) = 0 n) = 0 | [div_base_case] |
Thm*  a: a: , n: , n:  . Rem(a;n;a rem n) . Rem(a;n;a rem n) | [rem_fun_sat_rem_nrel] |
Thm*  a: a: , n: , n:  , k: , k: . k . k (a (a  n) n)   k k n n a a | [div_lbound_1] |
Thm*  a: a: , n: , n:  , p,q: , p,q: . Div(a;n;p) . Div(a;n;p)   Div(a;n;q) Div(a;n;q)   p = q p = q | [div_unique] |
Thm*  a: a: , n: , n:  . . 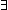 q: q: . Div(a;n;q) & (a . Div(a;n;q) & (a  n) = q n) = q | [div_elim] |
Thm*  a: a: , n: , n:  . Div(a;n;a . Div(a;n;a  n) n) | [div_fun_sat_div_nrel] |
Thm*  a: a: , n: , n:  . 0 . 0 (a (a  n) n) | [div_bounds_1] |
Thm*  a: a: , n:{...-1}. (a rem n) = (a rem -n) , n:{...-1}. (a rem n) = (a rem -n) | [rem_4_to_1] |
Thm*  a: a: , n:{...-1}. (a , n:{...-1}. (a  n) n)  {...0} {...0} | [division_typing2b_sfa] |
Thm*  a:{...0}, n:{...-1}. (a a:{...0}, n:{...-1}. (a  n) n)   | [division_typing2a_sfa] |
Thm*  a: a: , n: , n:  . (a . (a  n) n)   | [division_typing1a_sfa] |
Thm*  a: a: , b:{...-1}. (a , b:{...-1}. (a  b) = -(a b) = -(a  (-b)) (-b)) | [div_4_to_1] |
Thm*  a: a: , n:{...-1}. (a rem n) , n:{...-1}. (a rem n)   (-n) (-n) | [rem_bounds_4_typing_sfa] |
Thm*  a: a: , n: , n:  . (a rem n) . (a rem n)   n n | [rem_bounds_1_typing_sfa] |
Thm*  a: a: , n:{...-1}. 0 , n:{...-1}. 0 (a rem n) & (a rem n)<-n (a rem n) & (a rem n)<-n | [rem_bounds_4] |
Thm*  a: a: , n: , n:  . 0 . 0 (a rem n) & (a rem n)<n (a rem n) & (a rem n)<n | [rem_bounds_1] |
Thm*  a,b: a,b: . (a -- (a -- b)) = imin(a;b) . (a -- (a -- b)) = imin(a;b) | [ndiff_ndiff_eq_imin] |
Thm*  a,b: a,b: , c: , c: . ((a -- b) -- c) = (a -- (b+c)) . ((a -- b) -- c) = (a -- (b+c)) | [ndiff_ndiff] |
Thm*  a: a: , b: , b: . ((a+b) -- b) = a . ((a+b) -- b) = a | [ndiff_inv] |
Thm*  a: a: . (0 -- a) = 0 . (0 -- a) = 0 | [ndiff_ann_l] |
Thm*  a: a: . (a -- 0) = a . (a -- 0) = a | [ndiff_id_r] |
Thm*  P:( P:(  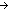 Prop). ( Prop). ( x: x: . P(|x|)) . P(|x|))   ( ( x: x: . P(x)) . P(x)) | [absval_elim] |
Thm*  i: i: , n: , n: . |i|>n . |i|>n   i<-n i<-n 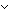 i>n i>n | [absval_lbound] |
Thm*  i: i: , n: , n: . |i| . |i| n n   -n -n i & i i & i n n | [absval_ubound] |
Thm*  i: i: . |i| = i . |i| = i | [absval_pos] |
Thm*  x: x: . |x| . |x|   | [absval_wf] |
Thm*  i,j: i,j: . i . i j j   | [multiply_nat_wf] |
Thm*  a,b: a,b: . 0 . 0 a a b b | [mul_bounds_1a] |
Thm*  i1,i2,j1,j2: i1,i2,j1,j2: . i1 . i1 j1 j1   i2 i2 j2 j2   i1 i1 i2 i2 j1 j1 j2 j2 | [multiply_functionality_wrt_le] |
Thm*  a,b: a,b: , n: , n: . a . a b b   n n a a n n b b | [mul_preserves_le] |
Def Rem(a;n;r) == 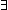 q: q: . Div(a;n;q) & q . Div(a;n;q) & q n+r = a n+r = a | [rem_nrel] |