| Rank | Theorem | Name |
| 4 |
Thm*  a: a: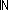 , b:{...-1}. (a , b:{...-1}. (a 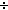 b) = -(a b) = -(a 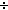 (-b)) (-b)) | [div_4_to_1] |
| cites |
| 0 |
Thm*  a: a: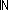 , n:{...-1}. 0 , n:{...-1}. 0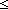 (a rem n) & (a rem n) < -n (a rem n) & (a rem n) < -n | [rem_bounds_4] |
| 0 |
Thm*  a: a: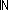 , n: , n: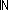 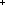 . 0 . 0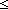 (a rem n) & (a rem n) < n (a rem n) & (a rem n) < n | [rem_bounds_1] |
| 0 |
Thm*  a: a: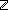 , n: , n: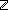  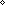 . a = (a . a = (a 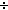 n) n)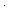 n+(a rem n) n+(a rem n) | [div_rem_sum] |
| 1 |
Thm*  a,b,n: a,b,n: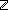 . a = b . a = b 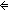 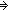 a+n = b+n a+n = b+n | [add_mono_wrt_eq] |
| 3 |
Thm*  a,b,n: a,b,n: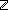 . a < b . a < b 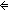 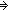 a+n < b+n a+n < b+n | [add_mono_wrt_lt] |
| 2 |
Thm*  a,b,n: a,b,n: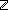 . a . a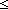 b b 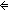 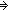 a+n a+n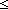 b+n b+n | [add_mono_wrt_le] |
| 0 | Thm*  i,j,k: i,j,k: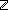 . i . i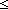 j j 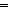 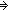 j < k j < k 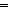 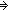 i < k i < k | [lt_transitivity_2] |
| 2 |
Thm*  a,b: a,b: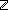 , n: , n: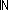 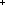 . n . n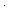 a < n a < n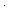 b b 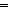 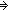 a < b a < b | [mul_cancel_in_lt] |
| 0 | Thm*  i,j: i,j: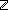 . i > j . i > j 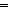  -i < -j -i < -j | [minus_functionality_wrt_lt] |