Thm*  f:(A f:(A  A A  A), u:A. A), u:A.
Thm* is_ident(A; f; u)
Thm*  
Thm* is_assoc_sep(A; f)
Thm*  
Thm* ( a,c,b: a,c,b: , e:({a..b , e:({a..b } }  A). A).
Thm* (a c c
Thm* ( 
Thm* (c<b
Thm* ( 
Thm* ((Iter(f;u) i:{a..b }. e(i)) }. e(i))
Thm* (=
Thm* (f((Iter(f;u) i:{a..c }. e(i)),f(e(c),Iter(f;u) i:{c+1..b }. e(i)),f(e(c),Iter(f;u) i:{c+1..b }. e(i)))) }. e(i)))) | [iter_via_intseg_split_pluck] |
Thm*  f:(A f:(A  A A  A), u:A. A), u:A.
Thm* is_ident(A; f; u)
Thm*  
Thm* is_assoc_sep(A; f)
Thm*  
Thm* ( a,b: a,b: , c:{a...b}, d:{c..b , c:{a...b}, d:{c..b }, e:({a..b }, e:({a..b } }  A). A).
Thm* (( i:{a..b i:{a..b }. i<c }. i<c 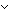 d d i i   e(i) = u) e(i) = u)
Thm* ( 
Thm* ((Iter(f;u) i:{a..b }. e(i)) = (Iter(f;u) i:{c..d }. e(i)) = (Iter(f;u) i:{c..d }. e(i))) }. e(i))) | [iter_via_intseg_amputate_units] |
Thm*  f:(A f:(A  A A  A), u:A. A), u:A.
Thm* is_ident(A; f; u)
Thm*  
Thm* is_assoc_sep(A; f)
Thm*  
Thm* ( a,c,b: a,c,b: , e:({a..b , e:({a..b } }  A). A).
Thm* (a c c
Thm* ( 
Thm* (c b b
Thm* ( 
Thm* ((Iter(f;u) i:{a..b }. e(i)) }. e(i))
Thm* (=
Thm* (f((Iter(f;u) i:{a..c }. e(i)),Iter(f;u) i:{c..b }. e(i)),Iter(f;u) i:{c..b }. e(i))) }. e(i))) | [iter_via_intseg_split_mid] |
Thm*  f:(A f:(A  A A  A), u:A. A), u:A.
Thm* is_commutative_sep(A; f)
Thm*  
Thm* is_ident(A; f; u)
Thm*  
Thm* is_assoc_sep(A; f)
Thm*  
Thm* ( a,b: a,b: , e,g:({a..b , e,g:({a..b } }  A). A).
Thm* (f((Iter(f;u) i:{a..b }. e(i)),Iter(f;u) i:{a..b }. e(i)),Iter(f;u) i:{a..b }. g(i)) }. g(i))
Thm* (=
Thm* ((Iter(f;u) i:{a..b }. f(e(i),g(i))) }. f(e(i),g(i)))
Thm* (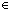 A) A) | [iter_via_intseg_comp_binop] |
Thm* is_assoc_sep( ; ( ; (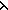 x,y. x+y)) x,y. x+y)) | [is_assoc_intadd] |
Thm* is_assoc_sep( ; ( ; (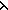 x,y. x x,y. x y)) y)) | [is_assoc_intmul] |