Selected Objects
| THM | cons_neq_nil |
 h:T, t:T List. h:T, t:T List. 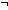 h.t = nil h.t = nil |
| COM | LIST_DEFS |
BASIC LIST FUNCTIONS
... |
| def | null |
null(as) == Case of as; nil  true true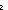 ; a.as' ; a.as'  false false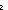 |
| THM | assert_of_null |
 as:T List. null(as) as:T List. null(as) 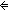 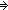 as = nil as = nil |
| def | append |
as @ bs == Case of as; nil  bs ; a.as' bs ; a.as'  a.(as' @ bs) (recursive) a.(as' @ bs) (recursive) |
| THM | append_assoc |
 as,bs,cs:T List. ((as @ bs) @ cs) = (as @ (bs @ cs)) as,bs,cs:T List. ((as @ bs) @ cs) = (as @ (bs @ cs)) |
| THM | append_back_nil |
 as:T List. (as @ nil) = as as:T List. (as @ nil) = as |
| def | length |
||as|| == Case of as; nil  0 ; a.as' 0 ; a.as'  ||as'||+1 (recursive) ||as'||+1 (recursive) |
| THM | length_cons |
 a:A, as:A List. ||a.as|| = ||as||+1 a:A, as:A List. ||a.as|| = ||as||+1 |
| THM | length_nil |
||nil|| = 0 |
| THM | non_neg_length |
 l:A List. ||l|| l:A List. ||l||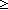 0 0 |
| THM | pos_length |
 l:A List. l:A List. 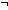 l = nil l = nil 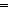 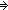 ||l|| ||l||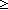 1 1 |
| THM | length_append |
 as,bs:T List. ||as @ bs|| = ||as||+||bs|| as,bs:T List. ||as @ bs|| = ||as||+||bs|| |
| THM | length_of_not_nil |
 as:A List. as:A List. 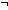 as = nil as = nil 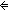 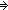 ||as|| ||as||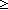 1 1 |
| THM | length_of_null_list |
 as:A List. as = nil as:A List. as = nil 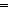 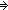 ||as|| = 0 ||as|| = 0 |
| def | map |
map(f;as) == Case of as; nil  nil ; a.as' nil ; a.as'  f(a).map(f;as') (recursive) f(a).map(f;as') (recursive) |
| THM | map_length |
 f:(A f:(A 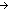 B), as:A List. ||map(f;as)|| = ||as|| B), as:A List. ||map(f;as)|| = ||as|| |
| THM | map_map |
 f:(A f:(A 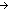 B), g:(B B), g:(B 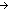 C), as:A List. map(g;map(f;as)) = map(g o f;as) C), as:A List. map(g;map(f;as)) = map(g o f;as) |
| THM | map_append |
 f:(A f:(A 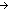 B), as,as':A List. map(f;as @ as') = (map(f;as) @ map(f;as')) B), as,as':A List. map(f;as @ as') = (map(f;as) @ map(f;as')) |
| THM | map_id |
 as:A List. map(Id;as) = as as:A List. map(Id;as) = as |
| def | hd |
hd(l) == Case of l; nil  "?" ; h.t "?" ; h.t  h h |
| def | tl |
tl(l) == Case of l; nil  nil ; h.t nil ; h.t  t t |
| THM | length_tl |
 l:A List. ||l|| l:A List. ||l||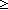 1 1 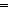 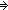 ||tl(l)|| = ||l||-1 ||tl(l)|| = ||l||-1 |
| def | nth_tl |
nth_tl(n;as) == if n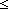 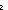 0 0 as else nth_tl(n-1;tl(as)) fi (recursive) as else nth_tl(n-1;tl(as)) fi (recursive) |
| THM | length_nth_tl |
 as:A List, n:{0...||as||}. ||nth_tl(n;as)|| = ||as||-n as:A List, n:{0...||as||}. ||nth_tl(n;as)|| = ||as||-n |
| def | reverse |
rev(as) == Case of as; nil  nil ; a.as' nil ; a.as'  rev(as') @ [a] (recursive) rev(as') @ [a] (recursive) |
| THM | reverse_append |
 as,bs:T List. rev(as @ bs) = (rev(bs) @ rev(as)) as,bs:T List. rev(as @ bs) = (rev(bs) @ rev(as)) |
| def | firstn |
firstn(n;as)
== Case of as; nil  nil ; a.as' nil ; a.as'  if 0< if 0<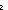 n n a.firstn(n-1;as') else nil fi a.firstn(n-1;as') else nil fi
(recursive) |
| THM | length_firstn |
 as:A List, n:{0...||as||}. ||firstn(n;as)|| = n as:A List, n:{0...||as||}. ||firstn(n;as)|| = n |
| def | segment |
as[m..n ] == firstn(n-m;nth_tl(m;as)) ] == firstn(n-m;nth_tl(m;as)) |
| THM | length_segment |
 as:T List, i:{0...||as||}, j:{i...||as||}. ||as[i..j as:T List, i:{0...||as||}, j:{i...||as||}. ||as[i..j ]|| = j-i ]|| = j-i |
| THM | eq_cons_imp_eq_tls |
 a,b:A, as,bs:A List. a.as = b.bs a,b:A, as,bs:A List. a.as = b.bs 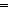 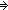 as = bs as = bs |
| THM | eq_cons_imp_eq_hds |
 a,b:A, as,bs:A List. a.as = b.bs a,b:A, as,bs:A List. a.as = b.bs 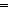 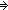 a = b a = b |
| def | select |
l[i] == hd(nth_tl(i;l)) |
| THM | select_cons_hd |
 a:T, as:T List, i: a:T, as:T List, i: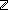 . i . i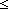 0 0 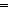 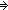 (a.as)[i] = a (a.as)[i] = a |
| THM | select_cons_tl |
 a:T, as:T List, i: a:T, as:T List, i: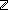 . 0<i . 0<i 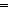 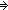 i i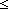 ||as|| ||as|| 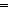 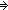 (a.as)[i] = as[(i-1)] (a.as)[i] = as[(i-1)] |
| THM | select_append_back |
 as,bs:T List, i:{||as||..(||as||+||bs||) as,bs:T List, i:{||as||..(||as||+||bs||) }. (as @ bs)[i] = bs[(i-||as||)] }. (as @ bs)[i] = bs[(i-||as||)] |
| THM | select_append_front |
 as,bs:T List, i: as,bs:T List, i: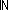 ||as||. (as @ bs)[i] = as[i] ||as||. (as @ bs)[i] = as[i] |
| THM | select_tl |
 as:A List, n: as:A List, n: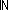 (||as||-1). tl(as)[n] = as[(n+1)] (||as||-1). tl(as)[n] = as[(n+1)] |
| THM | select_nth_tl |
 as:T List, n:{0...||as||}, i: as:T List, n:{0...||as||}, i: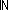 (||as||-n). nth_tl(n;as)[i] = as[(i+n)] (||as||-n). nth_tl(n;as)[i] = as[(i+n)] |
| THM | select_firstn |
 as:T List, n:{0...||as||}, i: as:T List, n:{0...||as||}, i: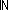 n. firstn(n;as)[i] = as[i] n. firstn(n;as)[i] = as[i] |
| def | reject |
as\[i] == if i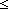 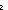 0 0 tl(as) else Case of as; nil tl(as) else Case of as; nil  nil ; a'.as' nil ; a'.as'  a'.as'\[i-1] fi a'.as'\[i-1] fi
(recursive) |
| THM | reject_cons_hd |
 a:T, as:T List, i: a:T, as:T List, i: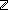 . i . i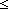 0 0 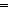 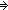 (a.as)\[i] = as (a.as)\[i] = as |
| THM | reject_cons_tl |
 a:T, as:T List, i: a:T, as:T List, i: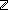 . 0<i . 0<i 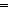 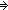 i i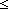 ||as|| ||as|| 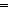 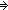 (a.as)\[i] = a.as\[i-1] (a.as)\[i] = a.as\[i-1] |
| THM | map_select |
 f:(A f:(A 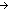 B), as:A List, n: B), as:A List, n: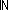 ||as||. map(f;as)[n] = f(as[n]) ||as||. map(f;as)[n] = f(as[n]) |
| COM | reduce_com |
============LIST FOLDING============ |
| def | reduce |
reduce(f;k;as) == Case of as; nil  k ; a.as' k ; a.as'  f(a,reduce(f;k;as')) f(a,reduce(f;k;as'))
(recursive) |
| def | for |
For{T,op,id} x 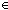 as. f(x) == reduce(op;id;map( as. f(x) == reduce(op;id;map(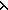 x:T. f(x);as)) x:T. f(x);as)) |
| def | mapcons |
mapcons(f;as) == Case of as; nil  nil ; a.as' nil ; a.as'  f(a,as').mapcons(f;as') f(a,as').mapcons(f;as')
(recursive) |
| def | for_hdtl |
ForHdTl{A,f,k} h::t 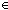 as. g(h;t) == reduce(f;k;mapcons( as. g(h;t) == reduce(f;k;mapcons(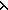 h,t. g(h;t);as)) h,t. g(h;t);as)) |
| def | listify |
f{m..n } == if n } == if n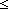 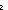 m m nil else f(m).f{(m+1)..n nil else f(m).f{(m+1)..n } fi (recursive) } fi (recursive) |
| THM | listify_length |
 m,n: m,n: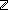 , f:({m..n , f:({m..n } } 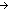 T). n<m T). n<m 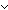 ||f{m..n ||f{m..n }|| = n-m }|| = n-m |
| THM | listify_select_id |
 as:T List. ( as:T List. (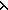 i: i: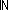 ||as||. as[i]){ ||as||. as[i]){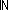 ||as||} = as ||as||} = as |
| THM | select_listify_id |
 n: n: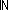 , f:( , f:(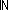 n n 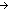 T), i: T), i: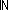 n. (f{ n. (f{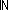 n})[i] = f(i) n})[i] = f(i) |
| COM | list_subtypes |
============LIST SUBTYPE============ |
| def | list_n |
A List(n) == {x:(A List)| ||x|| = n } |
| THM | list_n_properties |
 n: n: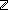 , as:A List(n). ||as|| = n , as:A List(n). ||as|| = n |
| COM | mapc_com |
====================CURRIED MAP FUNCTION====================Illustration of use of add_rec_def for a curried function |
| def | mapc |
mapc(f)(as) == Case of as; nil  nil ; a.as1 nil ; a.as1  f(a).mapc(f)(as1) (recursive) f(a).mapc(f)(as1) (recursive) |
| COM | list_append_ind_com |
Alternative Induction Principle for ListsUsed for multiset induction. |
| THM | list_append_ind |
 Q:((T List) Q:((T List) 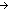 Prop). Prop).
Q(nil)
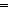 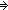
( x:T. Q([x])) x:T. Q([x]))
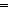 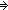
( ys,ys':T List. Q(ys) ys,ys':T List. Q(ys) 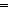 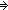 Q(ys') Q(ys') 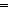 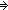 Q(ys @ ys')) Q(ys @ ys')) 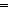 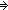 ( ( zs:T List. Q(zs)) zs:T List. Q(zs)) |