| 1 | 16. f: [[hd(ls)]] rho 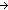 reduce( reduce(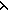 s,m. [[s]] rho s,m. [[s]] rho 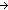 m;Prop;tl(ls)) m;Prop;tl(ls))
17. ||ls|| = ||v||+1 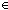 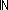
18.  i: i: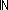 . i < ||v||+1 . i < ||v||+1 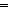 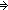 ls[i] ls[i] 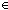 term_types(ds;st1;de;[u / v][i]) term_types(ds;st1;de;[u / v][i])
19.  ls:SimpleType List, f:reduce( ls:SimpleType List, f:reduce(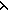 s,m. [[s]] rho s,m. [[s]] rho 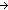 m;Prop;ls).
||ls|| = ||v|| m;Prop;ls).
||ls|| = ||v|| 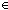 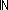 & ( & ( i: i: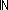 . i < ||v|| . i < ||v|| 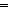 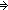 ls[i] ls[i] 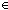 term_types(ds;st1;de;v[i])) term_types(ds;st1;de;v[i])) 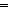 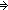 list_accum(x,t.x([[t]] e1 s s' a tr);f;v)
list_accum(x,t.x([[t]] e1 s s' a tr);f;v) 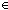 Prop Prop
20.  f:reduce( f:reduce(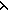 s,m. [[s]] rho s,m. [[s]] rho 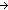 m;Prop;tl(ls)).
||tl(ls)|| = ||v|| m;Prop;tl(ls)).
||tl(ls)|| = ||v|| 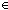 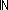 & ( & ( i: i: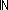 . i < ||v|| . i < ||v|| 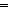 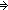 tl(ls)[i] tl(ls)[i] 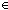 term_types(ds;st1;de;v[i])) term_types(ds;st1;de;v[i])) 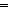 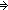 list_accum(x,t.x([[t]] e1 s s' a tr);f;v)
list_accum(x,t.x([[t]] e1 s s' a tr);f;v) 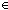 Prop Prop
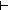 [[u]] e1 s s' a tr [[u]] e1 s s' a tr 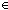 [[hd(ls)]] rho [[hd(ls)]] rho |