| 1 | 28. ||v2||+1 = ||v||+1  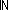
29.  i: i: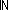 . i < ||v||+1 . i < ||v||+1   [u2 / v2][i] [u2 / v2][i]  term_types(ds;da;de;[u / v][i]) term_types(ds;da;de;[u / v][i])
30. ||v2||+1 = ||v1||+1  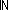 & ( & ( i: i: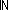 . i < ||v1||+1 . i < ||v1||+1   [u2 / v2][i] [u2 / v2][i]  term_types(ds;da;de;[u1 / v1][i])) term_types(ds;da;de;[u1 / v1][i]))
31.  i: i: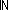 . i < ||v||+1 . i < ||v||+1   [[[u / v][i]]] e1 s1 a tr = [[[u1 / v1][i]]] e1 s1 s2 a tr [[[u / v][i]]] e1 s1 a tr = [[[u1 / v1][i]]] e1 s1 s2 a tr  [[[u2 / v2][i]]] rho [[[u2 / v2][i]]] rho
32. i: 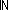
33. i < ||v||
34. [u2 / v2][(i+1)]  term_types(ds;da;de;[u / v][(i+1)]) term_types(ds;da;de;[u / v][(i+1)])
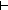 v2[i] v2[i]  term_types(ds;da;de;v[i]) term_types(ds;da;de;v[i]) |