Selected Objects
| THM | equal_functionality_wrt_subtype_rel |
 x,y:A. (A x,y:A. (A 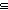 r B) r B)   x = y x = y   x = y x = y  B B |
| THM | subtype_rel_function |
(C 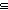 r A) r A)   (B (B 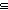 r D) r D)   ((A ((A  B) B) 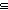 r (C r (C  D)) D)) |
| THM | subtype_rel_dep_function |
 B:(A B:(A  Type), C:Type, D:(C Type), C:Type, D:(C  Type). Type).
(C 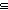 r A) r A)   ( ( a:C. B(a) a:C. B(a) 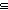 r D(a)) r D(a))   ((a:A ((a:A  B(a)) B(a)) 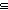 r (c:C r (c:C  D(c))) D(c))) |
| THM | subtype_rel_product |
 B:(A B:(A  Type), C:Type, D:(C Type), C:Type, D:(C  Type). Type).
(A 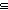 r C) r C)   ( ( a:A. B(a) a:A. B(a) 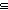 r D(a)) r D(a))   ((a:A ((a:A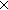 B(a)) B(a)) 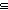 r (c:C r (c:C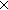 D(c))) D(c))) |
| THM | subtype_rel_list |
(A 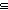 r B) r B)   ((A List) ((A List) 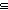 r (B List)) r (B List)) |
| THM | subtype_rel_transitivity |
(A 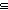 r B) r B)   (B (B 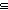 r C) r C)   (A (A 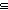 r C) r C) |
| def | strong-subtype |
strong-subtype(A;B)
== (A 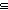 r B) r B)
== & ({b:B| 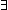 a:A. b = a a:A. b = a  B } B } 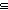 r A) r A)
== & ( a1,a2:A. a1 = a2 a1,a2:A. a1 = a2  B B   a1 = a2) a1 = a2) |
| THM | strong-subtype-self |
strong-subtype(A;A) |
| THM | strong-subtype_transitivity |
strong-subtype(A;B)   strong-subtype(B;C) strong-subtype(B;C)   strong-subtype(A;C) strong-subtype(A;C) |
| THM | subtype_rel_self |
A 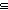 r A r A |
| THM | strong-subtype-set |
strong-subtype(A;B)
 
( P:(A P:(A  Prop), Q:(B Prop), Q:(B  Prop). Prop).
(( x:A. P(x) x:A. P(x)   Q(x)) Q(x))   strong-subtype({x:A| P(x) };{x:B| Q(x) })) strong-subtype({x:A| P(x) };{x:B| Q(x) })) |
| THM | strong-subtype-set2 |
 P:(A P:(A  Prop). strong-subtype({x:A| P(x) };A) Prop). strong-subtype({x:A| P(x) };A) |
| THM | strong-subtype-set3 |
 P:(A P:(A  Prop). strong-subtype(A;B) Prop). strong-subtype(A;B)   strong-subtype({x:A| P(x) };B) strong-subtype({x:A| P(x) };B) |
| THM | strong-subtype-l_member-type |
strong-subtype(A;B)   ( ( L:A List, x:B. (x L:A List, x:B. (x  L) L)   x x  A) A) |
| THM | strong-subtype-l_member |
strong-subtype(A;B)   ( ( L:A List, x:B. (x L:A List, x:B. (x  L) L)   (x (x  L)) L)) |
| THM | sq_stable__subtype_rel |
SqStable(A 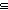 r B) r B) |
| THM | fun_exp_add_sq |
 n,m: n,m: , f,i:Top. (f^n+m(i)) ~ (f^n(f^m(i))) , f,i:Top. (f^n+m(i)) ~ (f^n(f^m(i))) |
| THM | maximal-in-list |
 f:(A f:(A  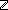 ), L:A List. 0<||L|| ), L:A List. 0<||L||   ( (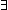 a a L.( L.( x x L.f(x) L.f(x) f(a))) f(a))) |
| THM | l_member_subtype |
 L:A List, x:A. (A L:A List, x:A. (A 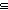 r B) r B)   (x (x  L) L)   (x (x  L) L) |
| def | l_interval |
l_interval(l;j;i) == mklist(i-j;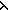 x.l[(j+x)]) x.l[(j+x)]) |
| THM | length_l_interval |
 l:T List, i: l:T List, i: ||l||, j: ||l||, j: (i+1). ||l_interval(l;j;i)|| = i-j (i+1). ||l_interval(l;j;i)|| = i-j  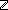 |
| THM | select_l_interval |
 l:T List, i: l:T List, i: ||l||, j: ||l||, j: (i+1), x: (i+1), x: (i-j). l_interval(l;j;i)[x] = l[(j+x)] (i-j). l_interval(l;j;i)[x] = l[(j+x)] |
| THM | hd_l_interval |
 l:T List, i: l:T List, i: ||l||, j: ||l||, j: i. hd(l_interval(l;j;i)) = l[j] i. hd(l_interval(l;j;i)) = l[j] |
| THM | last_l_interval |
 l:T List, i: l:T List, i: ||l||, j: ||l||, j: i. last(l_interval(l;j;i)) = l[(i-1)] i. last(l_interval(l;j;i)) = l[(i-1)] |
| def | pairwise |
( x,y x,y L.P(x;y)) == L.P(x;y)) ==  i: i: ||L||, j: ||L||, j: i. P(L[j];L[i]) i. P(L[j];L[i]) |
| THM | pairwise-cons |
 T:Type{i}, x:T, L:T List, P:(T T:Type{i}, x:T, L:T List, P:(T  T T  Prop{i'}). Prop{i'}).
( x,y x,y [x / L].P(x,y)) [x / L].P(x,y)) 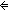  ( ( x,y x,y L.P(x,y)) & ( L.P(x,y)) & ( y y L.P(x,y)) L.P(x,y)) |
| THM | list-set-type |
 L:T List. L L:T List. L  {x:T| (x {x:T| (x  L) } List L) } List |
| THM | list-set-type2 |
 L:T List, P:(T L:T List, P:(T  Prop). ( Prop). ( x x L.P(x)) L.P(x))   L L  {x:T| P(x) } List {x:T| P(x) } List |
| THM | append_assoc_sq |
 as,bs,cs:Top List. ((as @ bs) @ cs) ~ (as @ bs @ cs) as,bs,cs:Top List. ((as @ bs) @ cs) ~ (as @ bs @ cs) |
| THM | inl_eq_inr |
 x:A, y:B. inl(x) = inr(y) x:A, y:B. inl(x) = inr(y)  A+B A+B   False False |
| def | finite-type |
finite-type(T) == 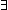 n: n: , f:( , f:( n n  T). Surj( T). Surj( n; T; f) n; T; f) |
| THM | finite-type-iff-list |
finite-type(T) 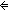  ( (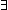 L:T List. L:T List.  x:T. (x x:T. (x  L)) L)) |
| THM | finite-set-type |
 P:(T P:(T  Prop). Prop).
( x:T. SqStable(P(x))) x:T. SqStable(P(x)))
 
(finite-type({x:T| P(x) }) 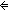  ( (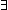 L:T List. L:T List.  x:T. P(x) x:T. P(x) 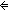  (x (x  L))) L))) |
| THM | finite-decidable-set |
 P:(T P:(T  Prop). Prop).
( x:T. Dec(P(x))) x:T. Dec(P(x)))
 
(finite-type({x:T| P(x) }) 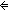  ( (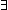 L:T List. L:T List.  x:T. P(x) x:T. P(x)   (x (x  L))) L))) |
| THM | map-map |
 as:Top List, f,g:Top. map(g;map(f;as)) ~ map(g o f;as) as:Top List, f,g:Top. map(g;map(f;as)) ~ map(g o f;as) |
| THM | map_is_nil |
 f:(A f:(A  B), l:A List. map(f;l) = nil B), l:A List. map(f;l) = nil 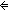  l = nil l = nil |
| THM | map-id |
 L:Top List. map( L:Top List. map(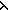 x.x;L) ~ L x.x;L) ~ L |
| THM | length-map |
 f:Top, T:Type, L:T List. ||map(f;L)|| ~ ||L|| f:Top, T:Type, L:T List. ||map(f;L)|| ~ ||L|| |
| THM | select-map |
 f:Top, T:Type, L:T List, i: f:Top, T:Type, L:T List, i: ||L||. map(f;L)[i] ~ (f(L[i])) ||L||. map(f;L)[i] ~ (f(L[i])) |
| THM | general_length_nth_tl |
 r: r: , L:Top List. ||nth_tl(r;L)|| = if r< , L:Top List. ||nth_tl(r;L)|| = if r<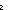 ||L|| ||L||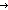 ||L||-r else 0 fi ||L||-r else 0 fi |
| def | mu |
mu(f) == if f(0)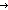 0 else mu( 0 else mu(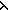 x.f(x+1))+1 fi (recursive) x.f(x+1))+1 fi (recursive) |
| THM | mu-property |
 f:( f:(   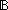 ). ( ). (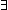 n: n: . f(n)) . f(n))   f(mu(f)) & ( f(mu(f)) & ( i: i: . i<mu(f) . i<mu(f)   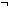 f(i)) f(i)) |
| def | upto |
upto(n) == if n=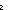 0 0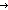 nil else upto(n-1) @ [(n-1)] fi (recursive) nil else upto(n-1) @ [(n-1)] fi (recursive) |
| THM | length_upto |
 n: n: . ||upto(n)|| ~ n . ||upto(n)|| ~ n |
| THM | upto_decomp |
 m: m: , n: , n: (m+1). upto(m) ~ (upto(n) @ map( (m+1). upto(m) ~ (upto(n) @ map(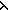 x.x+n;upto(m-n))) x.x+n;upto(m-n))) |
| THM | upto_iseg |
 i,j: i,j: . i . i j j   upto(i) upto(i)  upto(j) upto(j) |
| THM | select_upto |
 m: m: , n: , n: m. upto(m)[n] = n m. upto(m)[n] = n |
| THM | member_upto |
 n,i: n,i: . (i . (i  upto(n)) upto(n)) 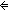  i<n i<n |
| THM | member_upto2 |
 n,i: n,i: . i<n . i<n   (i (i  upto(n)) upto(n)) |
| THM | before-upto |
 n: n: , x,y: , x,y: n. x before y n. x before y  upto(n) upto(n) 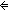  x<y x<y |
| THM | list-eq-set-type |
 P:(T P:(T  Prop), A,B:T List. Prop), A,B:T List.
A = B   ( ( i: i: ||A||. P(A[i])) ||A||. P(A[i]))   A = B A = B  {x:T| P(x) } List {x:T| P(x) } List |
| THM | before-map |
 f:(T f:(T  T'), L:T List, x',y':T'. T'), L:T List, x',y':T'.
x' before y'  map(f;L) map(f;L) 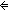  ( (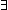 x,y:T. x before y x,y:T. x before y  L & f(x) = x' & f(y) = y') L & f(x) = x' & f(y) = y') |
| THM | filter_append_sq |
 P:(T P:(T  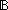 ), A:T List, B:Top. filter(P;A @ B) ~ (filter(P;A) @ filter(P;B)) ), A:T List, B:Top. filter(P;A @ B) ~ (filter(P;A) @ filter(P;B)) |
| THM | filter_map_upto |
 i,j: i,j: . .
i<j
 
( f:( f:(   T), P:(T T), P:(T  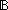 ). ).
(P(f(i))   ||filter(P;map(f;upto(i)))||<||filter(P;map(f;upto(j)))||) ||filter(P;map(f;upto(i)))||<||filter(P;map(f;upto(j)))||) |
| THM | filter_map_upto2 |
 t',m: t',m: , T:Type, f:( , T:Type, f:(   T), P:(T T), P:(T  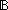 ). ).
m+1 ||filter(P;map(f;upto(t')))|| ||filter(P;map(f;upto(t')))||
 
(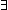 t: t: . P(f(t)) & ||filter(P;map(f;upto(t)))|| = m . P(f(t)) & ||filter(P;map(f;upto(t)))|| = m  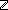 ) ) |
| THM | first0 |
 L:Top List. firstn(0;L) ~ nil L:Top List. firstn(0;L) ~ nil |
| THM | firstn_append |
 L1,L2:Top List, n: L1,L2:Top List, n: (||L1||+1). firstn(n;L1 @ L2) ~ firstn(n;L1) (||L1||+1). firstn(n;L1 @ L2) ~ firstn(n;L1) |
| THM | firstn_all |
 L:Top List, n: L:Top List, n: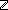 . ||L|| . ||L|| n n   (firstn(n;L) ~ L) (firstn(n;L) ~ L) |
| THM | firstn_map |
 f:(Top f:(Top  Top), n: Top), n: , l:Top List. firstn(n;map(f;l)) ~ map(f;firstn(n;l)) , l:Top List. firstn(n;map(f;l)) ~ map(f;firstn(n;l)) |
| THM | firstn_upto |
 n,m: n,m: . firstn(n;upto(m)) ~ if n . firstn(n;upto(m)) ~ if n 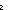 m m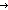 upto(n) else upto(m) fi upto(n) else upto(m) fi |
| def | concat |
concat(ll) == reduce(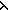 l,l'. l @ l';nil;ll) l,l'. l @ l';nil;ll) |
| THM | concat_append |
 ll1,ll2:(Top List) List. concat(ll1 @ ll2) ~ (concat(ll1) @ concat(ll2)) ll1,ll2:(Top List) List. concat(ll1 @ ll2) ~ (concat(ll1) @ concat(ll2)) |
| THM | concat-cons |
 l:Top List, ll:(Top List) List. concat([l / ll]) ~ (l @ concat(ll)) l:Top List, ll:(Top List) List. concat([l / ll]) ~ (l @ concat(ll)) |
| THM | select_concat |
 ll:(T List) List, n: ll:(T List) List, n: ||concat(ll)||. ||concat(ll)||.
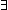 m: m: ||ll||. ||ll||.
||concat(firstn(m;ll))|| n n
& n-||concat(firstn(m;ll))||<||ll[m]||
& concat(ll)[n] = ll[m][(n-||concat(firstn(m;ll))||)] |
| THM | member-concat |
 ll:(T List) List, x:T. (x ll:(T List) List, x:T. (x  concat(ll)) concat(ll)) 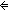  ( (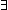 l:T List. (l l:T List. (l  ll) & (x ll) & (x  l)) l)) |
| THM | l_member_decomp |
 l:T List, x:T. (x l:T List, x:T. (x  l) l) 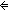  ( (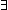 l1,l2:T List. l = (l1 @ [x] @ l2)) l1,l2:T List. l = (l1 @ [x] @ l2)) |
| THM | concat_iseg |
 ll1,ll2:(T List) List. ll1 ll1,ll2:(T List) List. ll1  ll2 ll2   concat(ll1) concat(ll1)  concat(ll2) concat(ll2) |
| THM | concat_map_upto |
 f:( f:(   (T List)), t,t': (T List)), t,t': . .
t<t'   concat(map(f;upto(t))) @ (f(t)) concat(map(f;upto(t))) @ (f(t))  concat(map(f;upto(t'))) concat(map(f;upto(t'))) |
| def | Id |
Id == Atom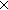  |
| THM | Id_sq |
SQType(Id) |
| def | mkid |
x_n == <x,n> |
| def | IdLnk |
IdLnk == Id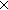 Id Id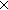  |
| THM | IdLnk_sq |
SQType(IdLnk) |
| def | lnk-inv |
lnk-inv(l) == <1of(2of(l)),1of(l),2of(2of(l))> |
| THM | lnk-inv-inv |
 l:IdLnk. lnk-inv(lnk-inv(l)) = l l:IdLnk. lnk-inv(lnk-inv(l)) = l  IdLnk IdLnk |
| def | Msg |
Msg(M) == l:IdLnk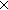 t:Id t:Id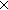 M(l,t) M(l,t) |
| COM | msg |
msg(l;t;v) == <l,t,v> |
| def | mlnk |
mlnk(m) == 1of(m) |
| def | mtag |
mtag(m) == 1of(2of(m)) |
| def | haslink |
haslink(l; m) == mlnk(m) = l |
| def | Msg_sub |
Msg_sub(l; M) == {m:Msg(M)| haslink(l; m) } |
| def | Knd |
Knd == (IdLnk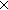 Id)+Id Id)+Id |
| THM | Knd_sq |
SQType(Knd) |
| def | isrcv |
isrcv(k) == isl(k) |
| def | islocal |
islocal(k) == 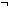 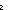 isl(k) isl(k) |
| THM | islocal-not-isrcv |
 k:Knd. islocal(k) ~ k:Knd. islocal(k) ~ 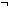 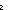 isrcv(k) isrcv(k) |
| def | rcv |
rcv(l; tg) == inl(<l,tg>) |
| def | locl |
locl(a) == inr(a) |
| THM | locl_one_one |
 a,b:Id. locl(a) = locl(b) a,b:Id. locl(a) = locl(b)   a = b a = b |
| THM | not_rcv_locl |
 a:Id, l:IdLnk, tg:Id. rcv(l; tg) = locl(a) a:Id, l:IdLnk, tg:Id. rcv(l; tg) = locl(a)   False False |
| THM | not_locl_rcv |
 a:Id, l:IdLnk, tg:Id. locl(a) = rcv(l; tg) a:Id, l:IdLnk, tg:Id. locl(a) = rcv(l; tg)   False False |