Selected Objects
| def | fpf-compatible |
f || g ==  x:A. x:A.  x x  dom(f) & dom(f) &  x x  dom(g) dom(g)   f(x) = g(x) f(x) = g(x)  B(x) B(x) |
| def | fpf-join |
f 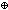 g == <1of(f) @ filter( g == <1of(f) @ filter( a. a.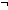 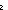 a a  dom(f);1of(g)), dom(f);1of(g)), a.f(a)?g(a)> a.f(a)?g(a)> |
| THM | fpf-join-dom |
 B:(A B:(A 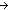 Type), eq:EqDecider(A), f,g:a:A fp-> B(a), x:A. Type), eq:EqDecider(A), f,g:a:A fp-> B(a), x:A.
x  dom(f dom(f 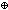 g) g) 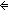  x x  dom(f) dom(f) 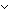 x x  dom(g) dom(g) |
| THM | fpf-join-dom2 |
 eq:EqDecider(A), f,g:a:A fp-> Top, x:A. eq:EqDecider(A), f,g:a:A fp-> Top, x:A.
x  dom(f dom(f 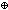 g) g) 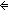  x x  dom(f) dom(f) 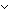 x x  dom(g) dom(g) |
| THM | fpf-join-is-empty |
 eq:EqDecider(A), f,g:x:A fp-> Top. eq:EqDecider(A), f,g:x:A fp-> Top.
fpf-is-empty(f 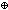 g) ~ (fpf-is-empty(f) g) ~ (fpf-is-empty(f)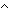 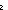 fpf-is-empty(g)) fpf-is-empty(g)) |
| THM | fpf-join-ap-sq |
 eq:EqDecider(A), f:a:A fp-> Top, g:Top, x:A. eq:EqDecider(A), f:a:A fp-> Top, g:Top, x:A.
f 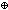 g(x) ~ if x g(x) ~ if x  dom(f) dom(f)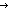 f(x) else g(x) fi f(x) else g(x) fi |
| def | fpf-single |
x : v == <[x], x.v> x.v> |
| THM | fpf-cap-single1 |
 eq:EqDecider(A), x:A, v,z:Top. x : v(x)?z ~ v eq:EqDecider(A), x:A, v,z:Top. x : v(x)?z ~ v |
| THM | fpf-ap-single |
 eq,x,v:Top. x : v(x) ~ v eq,x,v:Top. x : v(x) ~ v |
| THM | fpf-cap-single |
 eq:EqDecider(A), x,y:A, v,z:Top. x : v(y)?z ~ if eqof(eq)(x,y) eq:EqDecider(A), x,y:A, v,z:Top. x : v(y)?z ~ if eqof(eq)(x,y)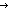 v else z fi v else z fi |
| THM | fpf-val-single1 |
 eq:EqDecider(A), x:A, v,P:Top. z != x : v(x) ==> P(a,z) ~ (True eq:EqDecider(A), x:A, v,P:Top. z != x : v(x) ==> P(a,z) ~ (True   P(x,v)) P(x,v)) |
| def | fpf-all |
 x x dom(f). v=f(x) dom(f). v=f(x)   P(x;v) == P(x;v) ==  x:A. x:A.  x x  dom(f) dom(f)   P(x;f(x)) P(x;f(x)) |
| THM | fpf-single-dom |
 eq:EqDecider(A), x,y:A, v:Top. x eq:EqDecider(A), x,y:A, v:Top. x  dom(y : v) dom(y : v) 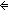  x = y x = y |
| THM | fpf-single-dom-sq |
 eq:EqDecider(A), x,y:A, v:Top. x eq:EqDecider(A), x,y:A, v:Top. x  dom(y : v) ~ (eqof(eq)(y,x)) dom(y : v) ~ (eqof(eq)(y,x)) |
| THM | fpf-all-single-decl |
 eq:EqDecider(A), P:(A eq:EqDecider(A), P:(A 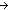 Type Type 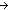 Prop), x:A, v:Type. Prop), x:A, v:Type.
 y y dom(x : v). w=x : v(y) dom(x : v). w=x : v(y)   P(y,w) P(y,w) 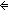  P(x,v) P(x,v) |
| THM | fpf-empty-compatible-right |
 eq:EqDecider(A), B:Top, f:a:A fp-> Top. f || eq:EqDecider(A), B:Top, f:a:A fp-> Top. f || |
| THM | fpf-empty-compatible-left |
 eq:EqDecider(A), B:Top, f:a:A fp-> Top. || f eq:EqDecider(A), B:Top, f:a:A fp-> Top. || f |
| def | fpf-dom-list |
fpf-dom-list(f) == 1of(f) |
| def | ma-state |
State(ds) == x:Id 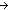 ds(x)?Top ds(x)?Top |
| def | ma-valtype |
ma-valtype(da; k) == da(k)?Top |
| def | msga |
MsgA
== ds:x:Id fp-> Type
==  da:a:Knd fp-> Type da:a:Knd fp-> Type
==  x:Id fp-> ds(x)?Void x:Id fp-> ds(x)?Void a:Id fp-> State(ds) a:Id fp-> State(ds) 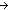 ma-valtype(da; locl(a)) ma-valtype(da; locl(a)) 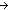 Prop Prop
== kx:Knd Id fp-> State(ds) Id fp-> State(ds) 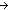 ma-valtype(da; 1of(kx)) ma-valtype(da; 1of(kx)) 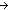 ds(2of(kx))?Void ds(2of(kx))?Void
== kl:Knd IdLnk fp-> (tg:Id IdLnk fp-> (tg:Id
== kl:Knd IdLnk fp-> ( IdLnk fp-> ( State(ds) State(ds) 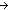 ma-valtype(da; 1of(kl)) ma-valtype(da; 1of(kl)) 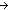
== kl:Knd IdLnk fp-> ((da(rcv(2of(kl); tg))?Void List)) List IdLnk fp-> ((da(rcv(2of(kl); tg))?Void List)) List
==  x:Id fp-> Knd List x:Id fp-> Knd List ltg:IdLnk ltg:IdLnk Id fp-> Knd List Id fp-> Knd List Top Top |
| def | ma-ds |
M.ds(x) == 1of(M)(x)?Top |
| def | ma-da |
M.da(a) == 1of(2of(M))(a)?Top |
| def | ma-decla |
a declared in M ==  locl(a) locl(a)  dom(1of(2of(M))) dom(1of(2of(M))) |
| def | da-outlink-f |
da-outlink-f(da;k) == <lnk(k),tag(k),da(k)> |
| def | da-outlinks |
da-outlinks(da;i)
== mapfilter( k.da-outlink-f(da;k); k.da-outlink-f(da;k); k.has-src(i;k);fpf-dom-list(da)) k.has-src(i;k);fpf-dom-list(da)) |
| THM | da-outlinks-empty |
 ltg:(IdLnk ltg:(IdLnk Id Id Type), i:Id. (ltg Type), i:Id. (ltg  da-outlinks(;i)) da-outlinks(;i))   False False |
| def | ma-outlinks |
ma-outlinks(M;i) == da-outlinks(1of(2of(M));i) |
| def | ma-din |
M.din(l,tg) == 1of(2of(M))(rcv(l; tg))?Top |
| def | ma-dout |
M.dout(l,tg) == 1of(2of(M))(rcv(l; tg))?Void |
| def | ma-init |
M.init(x,v) == x0 != 1of(2of(2of(M)))(x) ==> v = x0  1of(M)(x)?Void 1of(M)(x)?Void |
| def | ma-st |
M.state == State(1of(M)) |
| def | ma-v |
M.V(k) == ma-valtype(1of(2of(M)); k) |
| def | ma-npre |
unsolvable M.pre(a,s)
== P != 1of(2of(2of(2of(M))))(a) ==>  v:M.da(locl(a)). v:M.da(locl(a)). 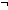 P(s,v) P(s,v) |
| def | ma-pre |
M.pre(a,s,v) == P != 1of(2of(2of(2of(M))))(a) ==> P(s,v) |
| def | ma-ef |
M.ef(k,x,s,v,w)
== E != 1of(2of(2of(2of(2of(M)))))(<k,x>) ==> w = E(s,v)  M.ds(x) M.ds(x) |
| def | tagged-list-messages |
tagged-list-messages(s;v;L)
== concat(map( tgf.map( tgf.map( x.<1of(tgf),x>;2of(tgf)(s,v));L)) x.<1of(tgf),x>;2of(tgf)(s,v));L)) |
| def | tagged-messages |
tagged-messages(l;s;v;L) == map( x.<l,x>;tagged-list-messages(s;v;L)) x.<l,x>;tagged-list-messages(s;v;L)) |
| def | ma-send |
M.send(k;l;s;v;ms;i)
== L != 1of(2of(2of(2of(2of(2of(M))))))(<k,l>) ==> ms
== L != 1of(2of(2of(2of(2of(2of(M))))))(<k,l>) ==> =
== L != 1of(2of(2of(2of(2of(2of(M))))))(<k,l>) ==> if source(l) = i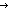
== L != 1of(2of(2of(2of(2of(2of(M))))))(<k,l>) ==> if concat(map( tgf.map( tgf.map( x. x.
== L != 1of(2of(2of(2of(2of(2of(M))))))(<k,l>) ==> if <1of(tgf),x>;2of(tgf)
== L != 1of(2of(2of(2of(2of(2of(M))))))(<k,l>) ==> if <1of(tgf),x>;(s
== L != 1of(2of(2of(2of(2of(2of(M))))))(<k,l>) ==> if <1of(tgf),x>;,v));L))
== L != 1of(2of(2of(2of(2of(2of(M))))))(<k,l>) ==> else nil fi
== L != 1of(2of(2of(2of(2of(2of(M))))))(<k,l>) ==>  (tg:Id (tg:Id
== L != 1of(2of(2of(2of(2of(2of(M))))))(<k,l>) ==>  ( ( if source(l) = i if source(l) = i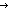
== L != 1of(2of(2of(2of(2of(2of(M))))))(<k,l>) ==>  ( ( if M.da(rcv(l; tg)) if M.da(rcv(l; tg))
== L != 1of(2of(2of(2of(2of(2of(M))))))(<k,l>) ==>  ( ( else Top fi) List else Top fi) List |
| def | ma-sends-on |
M sends on link l
== deq-member(IdLnkDeq;l;map( p.2of(p);1of(1of(2of(2of(2of(2of(2of(M))))))))) p.2of(p);1of(1of(2of(2of(2of(2of(2of(M))))))))) |
| def | ma-frame |
M.frame(k affects x)
== L != 1of(2of(2of(2of(2of(2of(2of(M)))))))(x) ==>  deq-member(KindDeq;k;L) deq-member(KindDeq;k;L) |
| def | ma-sframe |
M.sframe(k sends <l,tg>)
== L != 1of(2of(2of(2of(2of(2of(2of(2of(
== L != 1of(M))))))))(<l,tg>) ==>  deq-member(KindDeq;k;L) deq-member(KindDeq;k;L) |
| def | ma-sub |
M1 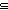 M2 M2
== 1of(M1) 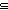 1of(M2) & 1of(2of(M1)) 1of(M2) & 1of(2of(M1)) 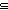 1of(2of(M2)) 1of(2of(M2))
== & 1of(2of(2of(M1))) 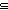 1of(2of(2of(M2))) 1of(2of(2of(M2)))
== & & 1of(2of(2of(2of(M1)))) 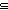 1of(2of(2of(2of(M2)))) 1of(2of(2of(2of(M2))))
== & & 1of(2of(2of(2of(2of(M1))))) 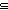 1of(2of(2of(2of(2of(M2))))) 1of(2of(2of(2of(2of(M2)))))
== & & 1of(2of(2of(2of(2of(2of(M1)))))) 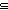 1of(2of(2of(2of(2of(2of(M2)))))) 1of(2of(2of(2of(2of(2of(M2))))))
== & & 1of(2of(2of(2of(2of(2of(2of(M1))))))) 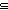 1of(2of(2of(2of(2of(2of(2of( 1of(2of(2of(2of(2of(2of(2of(
== & & 1of(2of(2of(2of(2of(2of(2of(M1)))))))  1of(M2))))))) 1of(M2)))))))
== & & 1of(2of(2of(2of(2of(2of(2of(2of(
== & & 1of(M1)))))))) 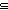 1of(2of(2of(2of(2of(2of(2of(2of(M2)))))))) 1of(2of(2of(2of(2of(2of(2of(2of(M2)))))))) |
| def | mk-ma |
mk-ma(ds; da; init; pre; ef; send; frame; sframe)
== <ds,da,init,pre,ef,send,frame,sframe,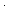 > > |
| def | ma-empty |
== mk-ma(; ; ; ; ; ; ; ) |
| def | ma-is-empty |
ma-is-empty(M)
== fpf-is-empty(1of(M))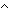 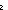 fpf-is-empty(1of(2of(M))) fpf-is-empty(1of(2of(M)))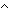 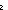
== fpf-is-empty(1of(2of(2of(M))))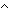 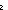 fpf-is-empty(1of(2of(2of(2of(M))))) fpf-is-empty(1of(2of(2of(2of(M)))))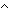 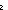
== fpf-is-empty(1of(2of(2of(2of(2of(M))))))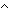 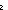
== fpf-is-empty(1of(2of(2of(2of(2of(2of(M)))))))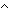 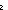
== fpf-is-empty(1of(2of(2of(2of(2of(2of(2of(M))))))))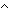 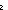
== fpf-is-empty(1of(2of(2of(2of(2of(2of(2of(2of(M))))))))) |
| def | ma-compatible-decls |
M1 ||decl M2 == 1of(M1) || 1of(M2) & 1of(2of(M1)) || 1of(2of(M2)) |
| def | ma-join |
M1 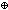 M2 M2
== mk-ma(1of(M1) 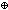 1of(M2); 1of(M2);
== mk-ma(1of(2of(M1)) 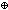 1of(2of(M2)); 1of(2of(M2));
== mk-ma(1of(2of(2of(M1))) 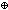 1of(2of(2of(M2))); 1of(2of(2of(M2)));
== mk-ma(1of(2of(2of(2of(M1)))) 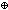 1of(2of(2of(2of(M2)))); 1of(2of(2of(2of(M2))));
== mk-ma(1of(2of(2of(2of(2of(M1))))) 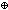 1of(2of(2of(2of(2of(M2))))); 1of(2of(2of(2of(2of(M2)))));
== mk-ma(1of(2of(2of(2of(2of(2of(M1)))))) 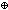 1of(2of(2of(2of(2of(2of(M2)))))); 1of(2of(2of(2of(2of(2of(M2))))));
== mk-ma(1of(2of(2of(2of(2of(2of(2of(M1))))))) 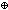 1of(2of(2of(2of(2of(2of(2of( 1of(2of(2of(2of(2of(2of(2of(
== mk-ma(1of(2of(2of(2of(2of(2of(2of(M1)))))))  1of(M2))))))); 1of(M2)))))));
== mk-ma(1of(2of(2of(2of(2of(2of(2of(2of(
== mk-ma(1of(M1)))))))) 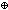 1of(2of(2of(2of(2of(2of(2of(2of(M2))))))))) 1of(2of(2of(2of(2of(2of(2of(2of(M2))))))))) |
| def | ma-compatible |
M1 || M2
== M1 ||decl M2
== & 1of(2of(2of(M1))) || 1of(2of(2of(M2)))
== & 1of(2of(2of(2of(M1)))) || 1of(2of(2of(2of(M2))))
== & 1of(2of(2of(2of(2of(M1))))) || 1of(2of(2of(2of(2of(M2)))))
== & 1of(2of(2of(2of(2of(2of(M1)))))) || 1of(2of(2of(2of(2of(2of(M2))))))
== & 1of(2of(2of(2of(2of(2of(2of(M1))))))) || 1of(2of(2of(2of(2of(2of(2of(
== & 1of(2of(2of(2of(2of(2of(2of(M1))))))) || 1of(M2)))))))
== & 1of(2of(2of(2of(2of(2of(2of(2of(
== & 1of(M1)))))))) || 1of(2of(2of(2of(2of(2of(2of(2of(M2)))))))) |
| def | ma-single-init |
x : t initially x = v == mk-ma(x : t; ; x : v; ; ; ; ; ) |
| def | ma-single-frame |
only members of L affect x :t == mk-ma(x : t; ; ; ; ; ; x : L; ) |
| def | ma-single-sframe |
only L sends on (l with tg) == mk-ma(; ; ; ; ; ; ; <l,tg> : L) |
| def | ma-single-effect |
ma-single-effect(ds; da; k; x; f) == mk-ma(ds; da; ; ; <k,x> : f; ; ; ) |
| def | ma-single-effect0 |
ma-single-effect0(x;A;k;T;f)
== ma-single-effect(x : A; k : T; k; x; ( s,v. f(s(x),v))) s,v. f(s(x),v))) |
| def | ma-single-effect1 |
ma-single-effect1(x;A;y;B;k;T;f)
== ma-single-effect(x : A 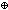 y : B; k : T; k; x; ( y : B; k : T; k; x; ( s,v. f(s(x),s(y),v))) s,v. f(s(x),s(y),v))) |
| def | ma-single-sends |
ma-single-sends(ds; da; k; l; f) == mk-ma(ds; da; ; ; ; <k,l> : f; ; ) |
| def | ma-single-sends1 |
ma-single-sends1(A; B; T; x; a; l; tg; f)
== ma-single-sends(x : A; a : B 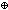 rcv(l; tg) : T; a; l; [<tg, rcv(l; tg) : T; a; l; [<tg, s,v. f(s(x),v)>]) s,v. f(s(x),v)>]) |
| def | ma-single-pre |
(with ds: ds
(action a:T
(precondition a(v) is
(P s v)
== mk-ma(ds; locl(a) : T; ; a : P; ; ; ; ) |
| def | ma-single-pre1 |
ma-single-pre1(x;A;a;T;y,v.P(y;v))
== (with ds: x : A
== (action a:T
== (precondition a(v) is
== ( 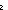 s,v. P(s(x);v) s v) s,v. P(s(x);v) s v) |
| def | ma-single-pre-init |
(with ds: ds
(init: init
action a:T
aprecondition a(v) is
aP)
== mk-ma(ds; locl(a) : T; init; a : P; ; ; ; ) |
| def | ma-single-pre-init1 |
ma-single-pre-init1(x;T;c;a;T';y,v.P(y;v))
== (with ds: x : T
== (init: x : c
== action a:T'
== aprecondition a(v) is
== a s,v. P(s(x);v)) s,v. P(s(x);v)) |
| def | ma-feasible |
Feasible(M)
==  x x dom(1of(M)). T=1of(M)(x) dom(1of(M)). T=1of(M)(x)   T T
== &  k k dom(1of(2of(M))). T=1of(2of(M))(k) dom(1of(2of(M))). T=1of(2of(M))(k)   Dec(T) Dec(T)
== &  a a dom(1of(2of(2of(2of(M))))). p=1of(2of(2of(2of(M))))(a) dom(1of(2of(2of(2of(M))))). p=1of(2of(2of(2of(M))))(a)  
== & s:State(1of(M)). Dec( s:State(1of(M)). Dec(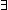 v:1of(2of(M))(locl(a))?Top. p(s,v)) v:1of(2of(M))(locl(a))?Top. p(s,v))
== &  kx kx dom(1of(2of(2of(2of(2of(M)))))). ef=1of(2of(2of(2of(2of(M)))))(kx) dom(1of(2of(2of(2of(2of(M)))))). ef=1of(2of(2of(2of(2of(M)))))(kx)  
== &M.frame(1of(kx) affects 2of(kx))
== &  kl kl dom(1of(2of(2of(2of(2of(2of(M))))))). dom(1of(2of(2of(2of(2of(2of(M))))))).
== & snd=1of(2of(2of(2of(2of(2of(M))))))(kl)    tg:Id. tg:Id.
== & (tg  map( map( p.1of(p);snd)) p.1of(p);snd))   M.sframe(1of(kl) sends <2of(kl),tg>) M.sframe(1of(kl) sends <2of(kl),tg>) |
| THM | ma-empty-feasible |
Feasible() |
| def | ma-frame-compatible |
ma-frame-compatible(A; B)
==  kx:(Knd kx:(Knd Id). Id).
== ( kx kx  dom(1of(2of(2of(2of(2of(A)))))) dom(1of(2of(2of(2of(2of(A))))))
== ( 
== (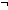  2of(kx) 2of(kx)  dom(1of(2of(2of(2of(2of(2of(2of(A)))))))) dom(1of(2of(2of(2of(2of(2of(2of(A))))))))
== ( 
== ( 2of(kx) 2of(kx)  dom(1of(2of(2of(2of(2of(2of(2of(B)))))))) dom(1of(2of(2of(2of(2of(2of(2of(B))))))))
== ( 
== ( deq-member(KindDeq;1of(kx);1of(2of(2of(2of(2of(2of(2of(B)))))))(2of(kx)))) deq-member(KindDeq;1of(kx);1of(2of(2of(2of(2of(2of(2of(B)))))))(2of(kx))))
== & ( kx kx  dom(1of(2of(2of(2of(2of(B)))))) dom(1of(2of(2of(2of(2of(B))))))
== & ( 
== & (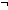  2of(kx) 2of(kx)  dom(1of(2of(2of(2of(2of(2of(2of(B)))))))) dom(1of(2of(2of(2of(2of(2of(2of(B))))))))
== & ( 
== & ( 2of(kx) 2of(kx)  dom(1of(2of(2of(2of(2of(2of(2of(A)))))))) dom(1of(2of(2of(2of(2of(2of(2of(A))))))))
== & ( 
== & ( deq-member(KindDeq;1of(kx);1of(2of(2of(2of(2of(2of(2of( deq-member(KindDeq;1of(kx);1of(2of(2of(2of(2of(2of(2of(
== & ( deq-member(KindDeq;1of(kx);1of(A)))))))(2of(kx)))) deq-member(KindDeq;1of(kx);1of(A)))))))(2of(kx)))) |
| def | ma-sframe-compatible |
ma-sframe-compatible(A; B)
==  kl:(Knd kl:(Knd IdLnk), tg:Id. IdLnk), tg:Id.
== ( kl kl  dom(1of(2of(2of(2of(2of(2of(A))))))) dom(1of(2of(2of(2of(2of(2of(A)))))))
== ( 
== ((tg  map( map( p.1of(p);1of(2of(2of(2of(2of(2of(A))))))(kl))) p.1of(p);1of(2of(2of(2of(2of(2of(A))))))(kl)))
== ( 
== (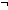  <2of(kl),tg> <2of(kl),tg>  dom(1of(2of(2of(2of(2of(2of(2of(2of(A))))))))) dom(1of(2of(2of(2of(2of(2of(2of(2of(A)))))))))
== ( 
== ( <2of(kl),tg> <2of(kl),tg>  dom(1of(2of(2of(2of(2of(2of(2of(2of(B))))))))) dom(1of(2of(2of(2of(2of(2of(2of(2of(B)))))))))
== ( 
== ( deq-member(KindDeq;1of(kl);1of(2of(2of(2of(2of(2of(2of(2of( deq-member(KindDeq;1of(kl);1of(2of(2of(2of(2of(2of(2of(2of(
== ( deq-member(KindDeq;1of(kl);1of(B))))))))(<2of(kl),tg>))) deq-member(KindDeq;1of(kl);1of(B))))))))(<2of(kl),tg>)))
== & ( kl kl  dom(1of(2of(2of(2of(2of(2of(B))))))) dom(1of(2of(2of(2of(2of(2of(B)))))))
== & ( 
== & ((tg  map( map( p.1of(p);1of(2of(2of(2of(2of(2of(B))))))(kl))) p.1of(p);1of(2of(2of(2of(2of(2of(B))))))(kl)))
== & ( 
== & (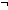  <2of(kl),tg> <2of(kl),tg>  dom(1of(2of(2of(2of(2of(2of(2of(2of(B))))))))) dom(1of(2of(2of(2of(2of(2of(2of(2of(B)))))))))
== & ( 
== & ( <2of(kl),tg> <2of(kl),tg>  dom(1of(2of(2of(2of(2of(2of(2of(2of(A))))))))) dom(1of(2of(2of(2of(2of(2of(2of(2of(A)))))))))
== & ( 
== & ( deq-member(KindDeq;1of(kl);1of(2of(2of(2of(2of(2of(2of(2of( deq-member(KindDeq;1of(kl);1of(2of(2of(2of(2of(2of(2of(2of(
== & ( deq-member(KindDeq;1of(kl);1of(A))))))))(<2of(kl),tg>))) deq-member(KindDeq;1of(kl);1of(A))))))))(<2of(kl),tg>))) |
| def | ma-compat |
A ||+ B == A || B & ma-frame-compatible(A; B) & ma-sframe-compatible(A; B) |
| def | ma-join-list |
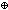 (L) == reduce( (L) == reduce( A,B. A A,B. A 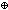 B;;L) B;;L) |
| def | msg-form |
MsgAForm
== x:Id fp-> Top x:Knd fp-> Type x:Knd fp-> Type x:Id fp-> Top x:Id fp-> Top x:Id fp-> Top x:Id fp-> Top x:Knd x:Knd Id fp-> Top Id fp-> Top
== x:Knd IdLnk fp-> Top IdLnk fp-> Top x:Id fp-> Top x:Id fp-> Top x:IdLnk x:IdLnk Id fp-> Top Id fp-> Top Top Top |
| THM | ma-single-init-feasible |
 x:Id, t:Type, v:t. Feasible(x : t initially x = v) x:Id, t:Type, v:t. Feasible(x : t initially x = v) |
| THM | ma-single-frame-feasible |
 x:Id, L:Knd List, t:Type. t x:Id, L:Knd List, t:Type. t   Feasible(only members of L affect x :t) Feasible(only members of L affect x :t) |
| THM | ma-single-sframe-feasible |
 l:IdLnk, tg:Id, L:Knd List. Feasible(only L sends on (l with tg)) l:IdLnk, tg:Id, L:Knd List. Feasible(only L sends on (l with tg)) |