| | Some definitions of interest. |
|
| da-outlinks | Def da-outlinks(da;i)
Def == mapfilter(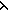 k.da-outlink-f(da;k); k.da-outlink-f(da;k);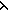 k.has-src(i;k);fpf-dom-list(da)) k.has-src(i;k);fpf-dom-list(da)) |
|
| da-outlink-f | Def da-outlink-f(da;k) == <lnk(k),tag(k),da(k)> |
|
| Kind-deq | Def KindDeq == union-deq(IdLnk Id;Id;product-deq(IdLnk;Id;IdLnkDeq;IdDeq);IdDeq) Id;Id;product-deq(IdLnk;Id;IdLnkDeq;IdDeq);IdDeq) |
|
| Knd | Def Knd == (IdLnk Id)+Id Id)+Id |
| | | Thm* Knd  Type Type |
|
| IdLnk | Def IdLnk == Id Id Id 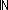 |
| | | Thm* IdLnk  Type Type |
|
| Id | Def Id == Atom 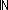 |
| | | Thm* Id  Type Type |
|
| has-src | Def has-src(i;k) == isrcv(k)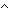 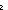 source(lnk(k)) = i source(lnk(k)) = i |
|
| assert | Def 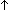 b == if b b == if b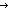 True else False fi True else False fi |
| | | Thm*  b: b: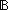 . b . b  Prop Prop |
|
| fpf | Def a:A fp-> B(a) == d:A List a:{a:A| (a a:{a:A| (a  d) } d) }  B(a) B(a) |
| | | Thm*  A:Type, B:(A A:Type, B:(A  Type). a:A fp-> B(a) Type). a:A fp-> B(a)  Type Type |
|
| fpf-join | Def f 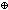 g == <1of(f) @ filter( g == <1of(f) @ filter(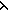 a. a.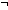  a a  dom(f);1of(g)), dom(f);1of(g)),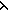 a.f(a)?g(a)> a.f(a)?g(a)> |
|
| fpf-dom | Def x  dom(f) == deq-member(eq;x;1of(f)) dom(f) == deq-member(eq;x;1of(f)) |
|
| fpf-dom-list | Def fpf-dom-list(f) == 1of(f) |
|
| iff | Def P 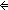 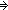 Q == (P Q == (P 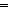 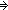 Q) & (P Q) & (P 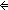 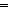 Q) Q) |
| | | Thm*  A,B:Prop. (A A,B:Prop. (A 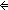 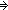 B) B)  Prop Prop |
|
| isrcv | Def isrcv(k) == isl(k) |
| | | Thm*  k:Knd. isrcv(k) k:Knd. isrcv(k)  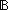 |
|
| l_member | Def (x  l) == l) == 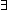 i: i: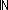 . i<||l|| & x = l[i] . i<||l|| & x = l[i]  T T |
| | | Thm*  T:Type, x:T, l:T List. (x T:Type, x:T, l:T List. (x  l) l)  Prop Prop |
|
| lnk | Def lnk(k) == 1of(outl(k)) |
| | | Thm*  k:Knd. isrcv(k) k:Knd. isrcv(k) 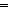 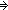 lnk(k) lnk(k)  IdLnk IdLnk |
|
| lsrc | Def source(l) == 1of(l) |
| | | Thm*  l:IdLnk. source(l) l:IdLnk. source(l)  Id Id |
|
| mapfilter | Def mapfilter(f;P;L) == map(f;filter(P;L)) |
| | | Thm*  T:Type, P:(T T:Type, P:(T  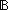 ), T':Type, f:({x:T| P(x) } ), T':Type, f:({x:T| P(x) }  T'), L:T List. T'), L:T List.
Thm* mapfilter(f;P;L)  T' List T' List |